|
Topic 6 – Alternative
Data Structures |
Spatial Reasoning
book |
Are You a GIS Dead Head? — describes
the structuring of traditional Raster data using implicit topology based on the
row/column positioning in a matrix
Raster is Faster, but Vector is Correcter — describes the structuring of
traditional Vector data using explicit topology linking spatial and attribute
tables
How are your QUADS and TINS?
— describes
alternative Quadtree and Triangular Irregular Network data formats
Rasterized Lines and Vectorized Cells — describes specialized offshoots of traditional raster and vector data
formats
<Click here> for a printer-friendly version of this topic
(.pdf).
(Back to the Table of Contents)
______________________________
Are You a
GIS Dead Head?
(GeoWorld, May 1995)
Even if
you're new to GIS, you may have encountered the scholarly skirmishes between
the raster heads and the vector heads.
Like other religious crusades, the principles in these debates often are
lost to mind-sets reflecting cultural exposure and past experience. More often than not, however, most of us just
become catatonic when the discussion turns to GIS data structures. But what the heck-it's worth another
try.
Let's
review the basic tenets of vector and raster data, then
extend this knowledge to the actual data structures involved. Vector data use sets of X,Y
coordinates to locate three basic types of landscape features: points, Iines, and areas.
For example, a typical water map identifies a spring as a dot (one X,Y coordinate pair), a stream as a squiggle (a set of
connected X,Y coordinates), and a lake as a glob (a set of connected X,Y
coordinates closing on itself and implying its interior). Raster data use an imaginary grid of cells to
represent the landscape. Point features
are stored as individual column/row entries in the grid; lines are identified
as a set of connected cells; and areas are distinguished as all of the cells
comprising a feature.
That
traditional representation constrains geographical phenomena to three
user-defined conditions (points, lines, and areas) and two GIS expressions
(vector and raster). I bet this
conceptual organization is fairly comfortable, and might even be familiar. But that's only half the problem— the
user/GIS representation has to be translated into a database/hardware
structure. At that step most of us
simply glaze over and leave such details to the GIS jocks. Actually, the concepts aren't too difficult
and they can help us understand much about different systems, the frustrations
we may encounter, and the future direction of GIS.
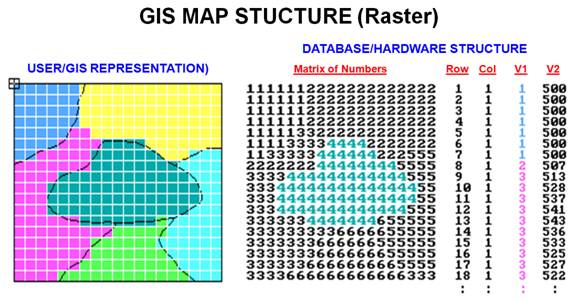
Figure
1. A file
containing a matrix of numbers (attribute values) characterizes each cell of an
imaginary grid. An alternative structure
uses a standard database file containing the column/row identifiers for each
cell followed by attribute fields, such as soil type and elevation.
Let's
consider some structures for raster data.
The left side of figure l shows an imaginary grid superimposed on a
typical soil map (more appropriately termed a "data layer'). The center portion of the figure identifies a
matrix of numbers with a numerical value assigned to each cell. In that case, the value represents a
particular type of soil, and its position in the matrix indicates its location.
To the computer, however, the matrix isn't a two dimensional array but simply
one long list of numbers. The first
number represents the upper-left corner of the matrix and the rest are ordered
from left to right, top to bottom.
Another map for the same area, say elevation, would be stored as a
separate ordered sequential file: This is the simplest and most frequently used
raster data structure.
An
offshoot of raster structure is used for most remote sensing data. Each cell in the grid represents a small area
of Earth's surface where a satellite collected spectral data. The numbers record relative amounts of
energy, such as blue, green, and red light radiating from the surface. The set of values for each energy level
represents a single data layer that can be arranged as a matrix and stored
separately. These data, however, are
stored more efficiently as an interlaced matrix, with all of the measurements
for each cell stored sequentially. For
example, the first three values might represent the blue, green, and red light
measurements for the upper-left cell, with the following triplets of values for
the other cells sequenced as before-left to right, top to bottom.
The
interlaced structure has a significant advantage in point-by-point processing,
because all information is contained in a single file and available as the
computer methodically steps through the matrix.
The computer doesn't have to open three separate files, then read blue,
green, and red values scattered all over the disk. As a result, you have a lot less disk
thrashing and a happier computer. That
may not seem like a big deal, but considering that a typical Landsat Thematic
Mapper scene contains seven data layers for about 36 million cells (that's more
than 250 million numbers), even a slight increase in storage efficiency is
cyber heaven.
The
interlaced structure might be neat and tidy for remote sensing data, but it's
inappropriate for a general GIS. First,
it's tough to add a new map. It means
extra room must be made to insert the new values by reading the first three
values from the original file, writing them to a new file, inserting the first
new value, and then repeating the process for the other million or so
cells. Oh yes, and then delete the
original file. And you have the same
problem if you want to delete a map.
Second, because the information for each data layer is dispersed (every
third value), it’s difficult to compress the redundancy found in a typical
map. Finally, any processing involving
neighboring cells requires extra work as the computer must continually jump
back and forth in the file to get values for the ceils above, below, right, and
left of the target ceil. In short, the
interlaced structure is best for specialized applications involving a fixed
number of maps constrained to cell-by-cell processing, such as most remote
sensing data processing.
So what
else do we have in raster structures?
Consider the right side of figure 1.
The structure uses a standard database file (a “database table")
with the column/row entries of the matrix explicitly stored as
"fields" (i.e., separate columns).
The subsequent fields contain the listing of values for various data
layers. Note that the set of soil values
under V1 corresponds to the left-hand column of the matrix. If there was room in the figure to list the
rest of the values in the field, the next set would replicate the next column
to the right in the matrix, then the next, and so on. The V2 listing depicts similarly organized
elevation values.
Now comes the advantage.
Suppose you want to find all locations (i.e., cells) that contain soil
type 4 and are more than 550 feet in elevation.
Simply enter a Structured Query Language (SQL) command and the computer
searches field columns V1 and V2 for the specified condition. A new field (V3) will be appended containing
the results. It's easy, because you use
a standard database file under the control of a standard database management
program. A standardized structure makes
it easy for GIS programmers, because they don't have to write all the code
that's already in the database "engine." Also, it allows you to store and process text
string designations, as well as numerical values. More importantly, it makes it easy on the
user, because the command uses the same format as a normal office
database.
The
problem lies with the computer. It hates
appending new fields to an existing table.
Also, the number of fields in a single table is constrained. The solution is a series of indexed tables,
with each cell's designation serving as the common link. With an indexed structure the computer can
easily "thread" from one table to another. Actually, there are good arguments for
storing each data layer as a separate indexed table. Creating, modifying, or deleting a map is a
breeze, because it affects only one table rather than a field embedded in a
complex table. That seems to brings us back to where we began— one map, one file. In that instance however, each map is a
standard indexed database table with all of the rights, privileges, and
responsibilities of your office database.
It puts raster GIS where it should be— right in the middle of standard
database technology. As we'll see in the
next section, vector GIS has been there all along.
Raster is
Faster, but Vector is Correcter
(GeoWorld, June 1995)
Your
computer really loves raster data— a cell on one map is at the same position on
all others. A couple of
"hits-to-disk" and it knows everything about a cell location. A few more hits up, down, left and right and
it knows everything about a location's entire neighborhood. In fact, it can "walk" from one
location to another and find everything it needs to know along the way, right
from the hard disk. Its world is
pre-defined in little byte-size pieces that are just
right.
However,
the computer-endearing qualities of consistency and uniformity put raster data
at odds with the human psyche (and a lot of reality). We see the unique character of each map
feature— a cute little jog here, a little bulge
there. The thought of generalizing these
details into a set of uniform globs is cartographic heresy.
So what
does it cost your computer, in terms of data structure, to retain the spatial
precision you demand? First, because
every map feature is unique, a complex data structure is required. Consistency and uniformity are out;
uniqueness and irregularity are in. More
importantly, processing involves threading through a series of linked files
(called "tables" in database speak), mathematically constructing map
features, calculating the implied coincidence, then reconstructing the new data
structure linkages; all that just to know the property line isn't 100 feet over
there ... picky, picky.
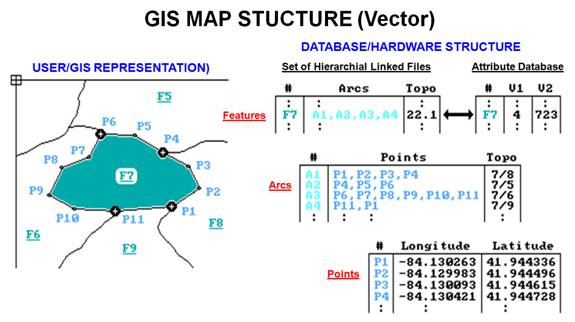
Figure
1 identifies the basic elements of vector data structure. It begins with a points table, attaching
coordinates to each point used in the construction of map features. Most systems use latitude and longitude as
their base coordinates. That's a good
choice, as it's a spherical coordinate system that accurately locates points
anywhere on Earth's surface. It's a
problem, however, when you want to relate points, such as measuring distances,
bearings, or planimetric areas.
Figure
1. A set
of f files links coordinates, arcs, and features to describe location. A
standard database file links each feature to its attributes, such as soil type
and elevation.
In
three dimensions, seemingly simple calculations involve solid geometry and ugly
equations that bring even powerful computers to their knees. Plus, the three-dimensional answers can't be
drawn on a flat screen. The solution is to
carry a user-specified map projection scheme and planar coordinate system
(e.g., Universal Transverse Mercator), then translate on-the.fly. Now the computer can work in any
two-dimensional rendering you choose and easily display the results on your screen
or plotter ... happy computer, happy you.
For
point features, the point table and its two-dimensional translation
specifications are linked directly to another indexed file containing
descriptive information, called "attributes," about each point. If this information depicted soil samples,
you could query the attribute table for all of the samples that have a pH less
than 7 and available phosphorus exceeding 30 parts per million. The results from the attribute query simply
"threads" to the coordinates of the subset of points meeting the
conditions, then plots them at blinding speed in the
vibrant color of your choice.
Line
and area features are a bit more complicated because the various connections
among sets of points need to be specified.
When you view a human-compatible map of water features you intuitively
note which stream is connected to which stream by the network of blue
squiggles. You note that lakes are blue
globs with a squiggle in and another out.
But the computer's point file is just a huge pile of unrelated
numbers. The first level of organization
is a linked arcs table. The file groups
the points into connected sets of arcs, forming the map features. In figure 1, points Pl, P2, P3, and P4 are
connected to form arc A1. Similarly,
arcs A2, A3, and A4 are defined by their linked coordinates.
The
features table puts it all together in geographic space by linking the “arcs” to actual map features. In the example, feature F7 is formed by
linking arcs A1, A2, A3, and A4. The
corresponding arcs table identifies which points are involved, with the
coordinates in the points table ultimately tying everything to the ground. At the top of this scheme is a linked info
table with the attribute data for each map feature. In the example, feature F7 is identified as
having soil type 4 (field V1) and an average elevation o1723 (field V2).
There,
that's not too bad—conceptually. The
tough part comes when you try to put it all into practice with about 100,000
polygons. That’s when each vendor's
"secret ingredients" of the general vector recipe take hold. Without giving away any corporate secrets,
let's take a look at some of the "tweaking" possibilities.
In
addition to the link to the points, the arc and feature tables often contain topological
and other information. For example, note
that arc A1 forms a shared boundary between features F7 and F8 as listed in the
"Topo" field of the arcs table (7/8). For maps composed of contiguous polygons
(e.g., soils, cover type, ownership, and census tracts) a search of this field
immediately identifies the adjoining neighbors for any map feature. Many systems store frequently used geometric
measurements— such areas as depicted in the "Topo"
field of the features table (22.1 acres).
The alternative to these tweaks in data-structure design is a lot of
computational thrashing and bashing each time they're needed.
Line
networks use topological information to establish which arcs are interconnected
and the nature of their connections. In
a stream network it depicts the direction of water flow. In a road network it characterizes all
possible routes from any location to ail other locations. To describe the linkage embedded fully,
however, a new element must be introduced: the “node.” These special points
are indicated in the figure as the large dots at the ends of each arc (P1, P4,
P6, and P11). Nodes represent locations
where things are changing, such as the separation of adjacent soil units along
a soil boundary. Some systems store
nodes in a separate table, while others simply give them special recognition in
the points table. The information
associated with a node reflects the type of data and the intended
processing.
If the
length of each arc is stored, the computer can find the distance from a
location to all other locations by simply summing the intervening arcs along a
route. If an average speed is stored for
each arc, the answer will be in travel-time.
But what about one-way streets and the relative difficulty of left and
right turns at each intersection or node? Attach that information to the nodes and the
computer will make the appropriate corrections as it encounters the
intersections along a route. Similarly,
an accumulated distance from a location to its surroundings can be determined
by keeping a running sum of the arc distances, respecting the
"turntable" information at each node.
Once that's known it's an easy matter to determine the optimal path
(shortest time or distance) from any location to the starting point.
All is for
naught, though, if your data structure hasn't been tweaked to carry the extra
topological and calibration information.
It should be apparent that, unlike raster data structures, vector data
structures can be radically different.
Ingenuity and programming dexterity are critical factors, as is the
matching of data design to intended applications and hardware. That's the tough part; there isn't a
universal truth in vector data structure.
The onus is on you to pick the right one for your applications, then understand it enough to take it to its limits.
How are your QUADS and TINS?
(GeoWorld, July 1995)
The
original raster and vector data structures have been around a long time. The basic concepts of representing a
landscape as a set of grid cells or a set of connected points are about as old
as cartography itself. The technical
refinements required for a functioning GIS, however, evolve continually. About the time I think we've reached the
pinnacle of data structure design, someone comes out with a new offshoot. The only folks who think they have it all are
overzealous marketers. The technical
types keep their heads down, constantly looking for more effective ways to
characterize mapped data.
Most
raster systems can perform run-length
compression, which compacts along the rows or the columns. For example, consider the matrix and its
row-compressed translation in Table 1. The
run-length data structure uses just 44 numbers to represent the 162 numbers in
the full matrix. It uses "value
through column” pairs of numbers to compact redundancy along a row. For example, the first row is read
"value from column 1 (assumed) through column 7, value 2 from column 8
(last column plus one) through column 17, and value 3 from column 18 through
column 18." That format is
particularly useful in map display.
Instead of "hitting disk" for the color-fill-pattern value at
each cell, the computer reads the pattern designation and simply repeats the
pattern specified by the column spread. That's a savings in storage and
increased performance-a win-win situation.
Table
1. Example of Run-Length Encoding (1 = Open Water, 2 =
Meadow, 3 =
Forest)
|
Full
Matrix |
Run-Length
(Row) Encoding |
|
111111122222222223 |
1,7,2,17,3,18 …1 thru 7, 2 thru 17, 3 thru 18 |
|
111111122222222233 |
1,7,2,16,3,18 …1 thru 7, 2 thru 16, 3 thru 18 |
|
111111122222222333 |
1,7,2,15,3,18 …1 thru 7, 2 thru 15, 3 thru 18 |
|
111111222222223333 |
1,6,2,14,3,18 …1 thru 6, 2 thru 14, 3 thru 18 |
|
111113333333333333 |
1,5,3,18 …1 thru 5, 3 thru 18 |
|
111113333333333333 |
1,5,3,18 …1 thru 5, 3 thru 18 |
|
111113333333333333 |
1,5,3,18 …1 thru 5, 3 thru 18 |
|
111333333333333333 |
1,3,3,18 …1 thru 3, 3 thru 18 |
|
111333333333333333 |
1,3,3,18 …1 thru 3, 3 thru 18 |
So why
don't we compress in the row and column directions at the same time and get
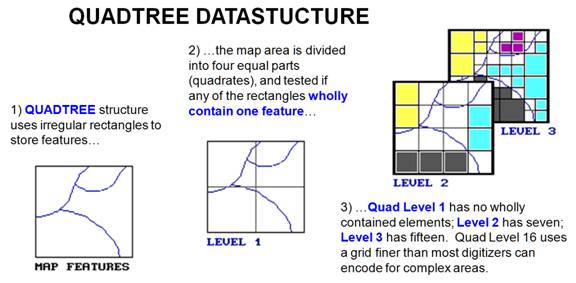
even more? In effect, that's what a quadtree data structure does. It's an interesting second cousin to the
traditional raster data structure that uses a cascading set of grid resolutions
to compress redundancy. Consider the
map boundaries shown in figure 1. If the
map window is divided in half in both the X and Y directions, four panels
(quadrants) are identified. That
superimposes a coarse grid of just two columns and two rows.
Figure
1.
Quadtree data structure elements.
At that
point the computer tests whether any quadrant wholly contains a single map
characteristic. In the example there are
none, so each of the panels is divided into its quads (Level 2). At that point, there are seven of the 16
quadrants that wholly contain a single characteristic. Their positions in the four-by-four grid are
noted, and the remaining nine mixed panels are divided into their quads (Level
3). Fourteen of these are noted as
completed, and the remaining 22 are divided for Level 4 of the quadtree. The process is repeated until an appropriate
quad level resolution is reached. At
level 16, a gridding resolution of 65,536 rows by 65,536 columns is available
wherever it is needed— that equates to a fixed raster grid of 4,294,967,296
cells! But the quadtree isn't forced to
use that resolution everywhere so it accurately stores most maps in less than a
megabyte.
Quadtrees and
run-length data structures are good at compressing raster data. However, they must be decompressed and then
recompressed for most map analysis operations.
Many GISs don't impose a compression routine within the data structure,
but simply leave it to commercial hard disk compression packages. Such packages respond to data redundancy and
optimize for disk head movement.
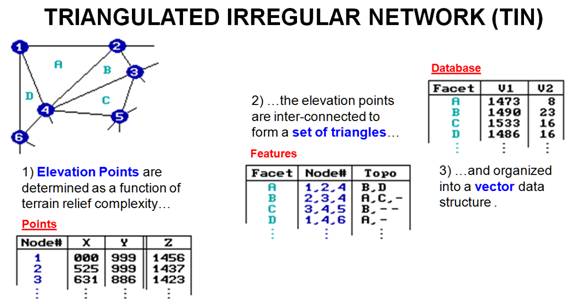
The Triangulated Irregular Network (TIN)
data structure is a vector offshoot originally designed for elevation
data. It avoids the redundancy of
elevations in a normal raster representation and is more efficient for some
terrain analysis operations, such as slope and aspect. It uses a set of irregularly spaced elevation
measurements with intensive sampling in areas of complex relief and/or important
features, such as ridges and streams. A
bit of computer wizardry is applied to determine the network of triangular
facets that best fits these data. Each
facet has three interconnected elevations and can be visualized as a tilted
triangular plane. The direction cosines
of the plane identify its slope and aspect.
The average of the three elevations generalizes the plane's height.
As
shown in figure 2, the XY coordinate (location) and the z coordinate
(elevation) are stored in a points table similar to traditional vector
structure. The triangular facets are
defined in a features table by their three nodes and adjoining facets. The final link is to an attribute table which
contains descriptive information on each facet.
Awesome shaded relief maps can be generated by plotting the facets in
3-D and shading them as functions of their slopes and aspects.
Figure
2. TIN
data structure elements.
Using a
TIN rather than raster structure to characterize a three-dimensional surface
has some significant advantages. It
usually requires fewer points, captures discontinuities such as streams and
ridges, and determines slope and aspect of the facet itself. It's the data structure of choice for most
civil engineering packages designed for terrain analysis. However, it's inappropriate for a generalized
GIS that mixes a variety of maps. First,
it's like raster, because it uses a mosaic of geographic chunks to represent a
map feature. The chunks are inconsistent
between maps, however, and something as simple as map overlay takes a severe
hit in performance. Also, TIN
two-dimensional renderings are complex and bewildering to most users compared
to a normal raster display or vector contour plot.
Quadtree
and TIN are useful offshoots of basic raster and vector data structures. They provide important benefits for certain
data under certain conditions. If they
match your needs, they're an invaluable addition to your GIS arsenal.
Rasterized Lines and Vectorized Cells
(GeoWorld, August 1995)
Chances
are your GIS is (or will be) ambidextrous.
It has a vector side and a raster side, and might even have TIN or quadtree
sides. The different data structures
indicate various perspectives on data types and user applications. The vector approach characterizes discrete
map objects and is influenced by applications in computer graphics. Raster characterizes continuous mapped data
and emerges from remote sensing applications that involve multivariate
statistics. Today, considerations in
database/hardware structure influence future development as much as historical
user/GIS representation theory. In a sense, the realities of an evolving
computer environment challenge traditional ways.
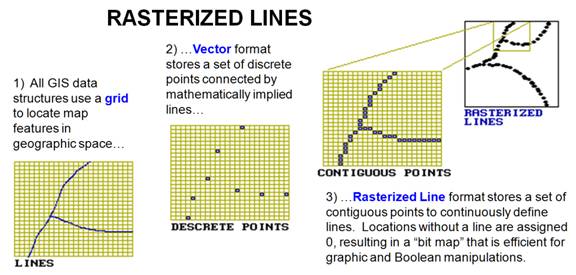
A rasterized lines structure is an
interesting offshoot from traditional data structures. It's sort of a hybrid because it uses a grid
structure to characterize a map's line work.
An optical scanner is used to “turn on” each cell in a fine sampling
matrix that corresponds to the set of lines.
The process is similar to the way your office fax machine “reads" a
document. The fax at the other end
simply deciphers the on-off conditions in the matrix and puts a dab of black
toner at spots corresponding to “on."
It skips over the "off" spots, leaving just white paper. That’s it, a black-and-white rendering of map
lines pushed over the phone lines.
If you
use a magnifying glass, you can see the individual dots. At normal viewing distances, however, they
merge to form smooth lines. Your brain
easily makes sense of the pattern of lines and implied polygons embedded in the
fine grid of the sampling matrix. Which streams are connected to which streams and which lakes are in
which watersheds are obvious from the graphic rendering.
But
that's not the case for a computer-the image is just a jumble of on and off
dots. The first step in imposing order
on data structure is to locate and mark as nodes all the special dots where
lines meet (intersections), or just hang out by themselves (end points). Traditional vector
structuring simply follows the dots between nodes and then storing the
coordinates for a point whenever there is a significant X or Y deflection. The result is a series of discrete points
connected by implied straight lines, as shown in inset 2 of figure 1. The nodes and intervening points then indexed
files, as described in the previous section.
Figure
1.
Rasterized lines data structure elements.
Rasterized
lines retain all the dots along the lines.
At first that seems stupid, because the points file is huge. Where an arc might require 10 discrete
points, a rasterized line might require 100 or more. Some tricks in data compression and
coordinate referencing can help, but it requires a lot more storage any way you
look at it. So why would anybody use a
rasterized line structure? Primarily
because it's a format hardware loves.
Faxes, scanners, screens, plotters and printers are based on dot
patterns. As a result, much attention is
paid to handling dotted data efficiently.
Also, advances in optical disk storage and memory chips are redefining
our concept of a "storage hog" so these files seem smaller each
year.
More
important, however, are advancements in central processing units (CPUs). Most computers still use a "kur-plunk-a" processing approach developed in the
1940s. It mimics our linear thinking and
the way we do things-do A, then B, then C.
Array and parallel processors, however, operate simultaneously on whole
sets of data, provided they're organized properly.
Suppose
you want to overlay a couple of traditional vector maps. In an instant, the computer reads the
coordinates for two points on one map, and then has to figure out if the
implied line segment between them crosses any implied line segment on the other
map. If it does, it mathematically
calculates the point of intersection, splits the two lines into four, and then
updates all the indexed tables.
Whew! That approach is a lot of
work, and it's a purely linear process and a mismatch for array
processing.
If the
data are in rasterized line format, however, an array processor merely reads
the corresponding chunks of cells on both maps and multiplies them together (a
Boolean operation for you techy types).
The product array identifies the composite of the two maps and
highlights the new nodes where lines cross.
Don't get me wrong: I'm not advocating you run out and buy rasterized
line systems, but they have some interesting features for tomorrow's computers.
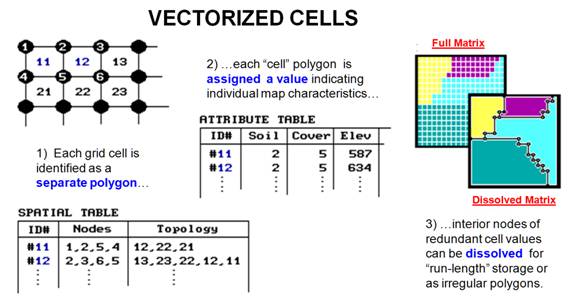
Another
interesting offshoot, vectorized cells,
cheats by storing each cell of an analysis grid as an individual polygon
(figure 2). It just so happens that all
of the polygons have the same square configuration and adjoin their neighbors. From a traditional vector perspective, each
point defining a cell is a node; each cell side is an arc composed of just two
nodes; and each cell is a polygonal feature composed of just four arcs. That approach uses the existing vector
structure without impacting the existing code.
It simply imposes consistency and uniformity in the polygons. All that's needed is an import module to
generate the appropriate configuration of vectorized cells and read the raster
values into a field in the corresponding attribute table. Raster-to-vector conversion can be completed
by dissolving the pseudo-boundaries between adjoining polygons with the same
value. Line features can be converted by
connecting the centers of cells with similar value. Point features are represented by the
coordinates of isolated cell centers.
Figure
2.
Vectorized cells data structure elements.
Vectorized
cells initially were used to "kludge" a link from raster to vector
systems. However, the inherent
consistency and uniformity of the structure (four points to a polygon), coupled
with advances in data compression and database technology, might spark a
resurgence in interest. Things as fluid because computers are becoming less bounded by
storage requirements and the industry is shifting toward new processors
and operating systems. Keep in mind that
there are only two things certain about data structures: (1) tomorrow there
will be new ones, and (2) what's good for one application isn't necessarily the
best for another.
_____________________