|
Topic 7 –
Spatial Data Mining in Geo-business |
GIS
Modeling book |
Twisting
the Perspective of Map Surfaces — describes the character of spatial
distributions through the generation of a customer density surface
Linking
Numeric and Geographic Distributions — investigates the link
between numeric and geographic distributions of mapped data
Myriad
Techniques Help to Interpolate Spatial Distributions — discusses
the basic concepts underlying spatial interpolation
Use
Map Analysis to Characterize Data Groups — describes the use of
“data distance” to derive similarity among the data patterns in a set of map
layers
Discover
the “Miracles” in Mapping Data Clusters — describes
the use of “clustering” to identify inherent groupings of similar data
patterns
The
Universal Key for Unlocking GIS’s Full Potential — outlines a
global referencing system approach compatible with standard DBMS systems
Further Reading
— four additional sections
<Click here>
for a printer-friendly version of this
topic (.pdf).
(Back to the Table of Contents)
______________________________
Twisting the Perspective of Map Surfaces
(GeoWorld, April 2008)
This section’s
theme grabs some earlier concepts, adds an eye of newt and then a twist of
perspective to concoct a slightly shaken (not stirred) new perception of map
surfaces. Traditionally one thinks of a
map surface in terms of a postcard scene of the
However,
a geomorphological point of view of a digital elevation model (DEM) isn’t the
only type of map surface. For example, a
Customer Density Surface can be
derived from sales data that depicts the peaks and valleys of customer
concentrations throughout a city as discussed in an earlier topic (see author’s
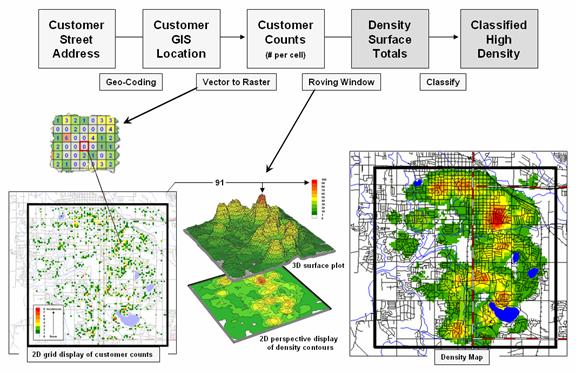
note). Figure 1 summarizes the
processing steps involved—1) a customer’s street address is geocoded to
identify its Lat/Lon coordinates, 2) vector to raster conversion is used to
place and aggregate the number of customers in each grid cell of an analysis
frame (discrete mapped data), 3) a
rowing window is used to count the total number of customers within a specified
radius of each cell (continuous mapped
data), and then 4) classified into logical ranges of customer density.
Figure 1. Geocoding can be used to connect customer
addresses to their geographic locations for subsequent map analysis, such as generating a map
surface of customer density.
The important
thing to note is that the peaks and valleys characterize the Spatial Distribution of the customers, a
concept closely akin to a Numerical
Distribution that serves as the foundation for traditional statistics. However in this instance, three dimensions
are needed to characterize the data’s dispersion—X and Y coordinates to
position the data in geographic space and a Z coordinate to indicate the
relative magnitude of the variable (# of customers). Traditional statistics needs only two
dimensions—X to identify the magnitude and Y to identify the number of
occurrences.
While
both perspectives track the relative frequency of occurrence of the values
within a data set, the spatial distribution extends the information to
variations in geographic space, as well as in numerical variations in
magnitude— from just “what” to “where is what.”
In this case, it describes the geographic pattern of customer density as
peaks (lots of customers nearby) and valleys (not many).
Within
our historical perspective of mapping the ability to plot “where is what” is an
end in itself. Like Inspector Columbo’s
crime scene pins poked on a map, the mere visualization of the pattern is
thought to be sufficient for solving crimes.
However, the volume of sales transactions and their subtle relationships
are far too complex for a visual (visceral?) solution using just a Google Earth
mashed-up image.
The
interaction of numerical and spatial distributions provides fertile turf for a better
understanding of the mounds of data we inherently collect every day. Each credit card swipe identifies a basket of
goods and services purchased by a customer that can place on a map for
grid-based map analysis to make sense of it all—“why” and “so what.”
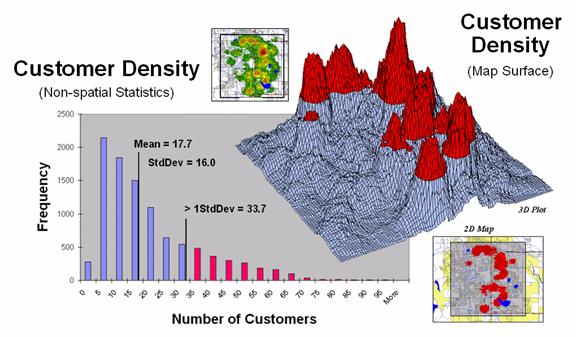
Figure 2. Merging traditional statistics and map
analysis techniques increases understanding of spatial patterns and relationships
(variance-focused; continuous) beyond the usual central tendency (mean-focused;
scalar) characterization of geo-business data.
For
example, consider the left side of figure 2 that relates the unusually high
response range of customers of greater than 1 standard deviation above the mean
(a numerical distribution perspective) to the right side that identifies the
location of these pockets of high customer density (a spatial distribution
perspective). As discussed in a previous
Beyond Mapping column (May 2002; see author’s note), this simple analysis uses
a typical transaction database to 1) map the customer locations, 2) derive a
map surface of customer density, 3) identify a statistic for determining
unusually high customer concentrations (> Mean + 1SD), and 4) apply the
statistic to locate the areas with lots of customers. The result is a map view of a commonly used
technique in traditional statistics—an outcome where the combined result of an
integrated spatial and numerical analysis is far greater than their individual
contributions.
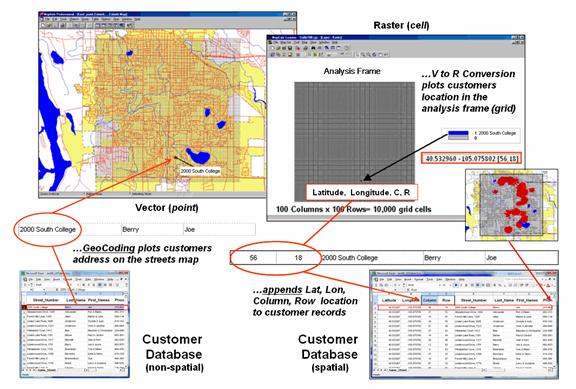
However,
another step is needed to complete the process and fully illustrate the
geo-business framework. The left side of
figure 3 depicts the translation of a non-spatial customer database into a
mapped representation using vector-based processing that determines Lat/Lon
coordinates for each record—the mapping component. Translation from vector to raster data
structure establishes the analytic frame needed for map analysis, such as
generating a customer density surface and classifying it into statistically
defined pockets of high customer density—then map analysis component.
Figure 3. The column, row index of the grid cells in
the analytic frame serves as a primary key for linking spatial analysis results
with individual records in a database.
The
importance of the analytic frame is paramount in the process as it provides the
link back to the original customer database—the spatial data mining
component. The column, row index of the
matrix for each customer record is appended to the database and serves as a
primary key for “walking” between the
Similarly,
maps of demographics, sales by product, travel-time to our store, and the like
can be used in customer segmentation and propensity modeling to identify maps
of future sales probabilities. Areas of
high probability can be cross-walked to an existing customer database (or zip
+4 or other generic databases) to identify new sales leads, product mix,
stocking levels, inventory management, and competition analysis. At the core of this vast potential for
geo-business application set is the analytic frame and its continuous map
surfaces that underwrite a spatially aware database.
_____________________________
Author’s Note: Related discussion on Density Surface
Analysis is presented in Beyond Mapping Compilation Series, book III, Topic 6,
section 2 “Milking
Spatial Context Information” posted at www.innovativegis.com.
Linking
Numeric and Geographic Distributions
(GeoWorld, June 2008)
The
previous section set the stage for discussion of the similarities and
differences of geo-business applications to more conventional GIS solutions in
municipalities, infrastructure, natural resources, and other areas with deep
roots in the mapping sciences.
Underlying the discussion was the concept of a Grid-based Analysis Frame that serves as a primary key for
“walking” between a continuous geographic space representation and the
individual records in a customer database.
It
illustrated converting a point map of customer locations into a Customer Density Surface that depicts
the “peaks and valleys” of customer concentrations throughout a city. While the process is analogous to Inspector
Columbo’s crime scene pins poked on a map, the mere visualization of a point
pattern is rarely sufficient for solving crimes. Nor is it adequate for a detailed
understanding of customer distribution and spatial relationships, such as
determining areas of statistically high concentrations—Customer Pockets—that can
be used in targeted marketing, locating ATMs or sales force allocation.
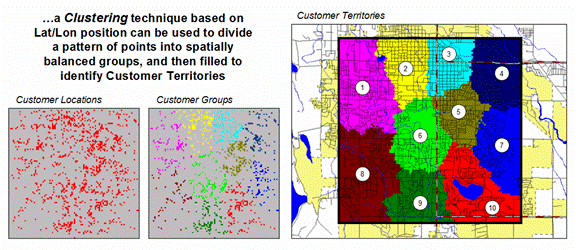
Another
grid-based technique for investigating the customer pattern involves
Figure 1. Clustering on the latitude and longitude
coordinates of point locations can be used to identify geographically balanced
customer territories.
The two
small inserts on the left show the general pattern of customers, and then the
partitioning of the pattern into spatially balanced groups. This initial step was achieved by applying a K-means
clustering algorithm to the latitude and longitude coordinates of the customer
locations. In effect this procedure
maximizes the differences between the groups while minimizing the differences
within each group. There are several
alternative approaches that could be applied, but K-means is an often-used
procedure that is available in all statistical packages and a growing number of
GIS systems.
The
final step to assign territories uses a nearest neighbor interpolation
algorithm to assign all non-customer locations to the nearest customer
group. The result is the customer
territories map shown on the right. The
partitioning based on customer locations is geographically balanced
(approximately the same area in each cluster), however it doesn’t consider the
number of customers within each group—that varies from 69 in the lower right
(Territory #8) to 252 (Territory #5) near the upper right… that twist of map
analysis will be tackled in a future beyond mapping column.
However
it does bring up an opportunity to discuss the close relationship between
spatial and non-spatial statistics. Most
of us are familiar with the old “bell-curve” for school grades. You know, with lots of C’s, fewer B’s and
D’s, and a truly select set of A’s and F’s.
Its shape is a perfect bell, symmetrical about the center with the tails
smoothly falling off toward less frequent conditions.
However
the normal
distribution (bell-shaped) isn’t as normal (typical) as you might
think. For example, Newsweek noted that the average grade at a major ivy-league
university isn’t a solid C with a few A’s and F’s sprinkled about as you might
imagine, but an A- with a lot of A’s trailing off to lesser amounts of B’s, C’s
and (heaven forbid) the very rare D or F.
Figure
2. Mapped data are characterized by
their geographic distribution (maps on the left) and their numeric distribution
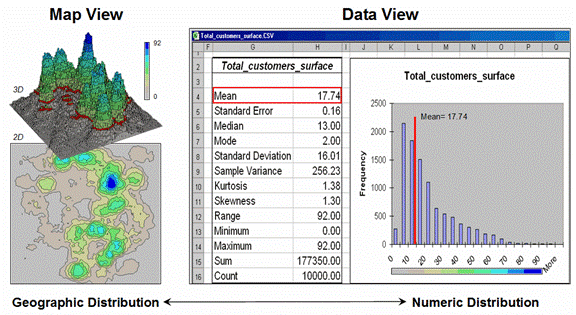
(descriptive statistics and histogram on the right).
The
frequency distributions of mapped data also tend toward the ab-normal (formally termed asymmetrical). For example, consider the customer density
data shown in the figure 2 that was derived by counting the total number of
customers within a specified radius of each cell (roving window). The geographic distribution of the data is
characterized in the Map View by the 2D contour map and
3D surface on the left. Note the
distinct pattern of the terrain with bigger bumps (higher customer density) in
the central portion of the project area.
As is normally the case with mapped data, the map values are neither
uniformly nor randomly distributed in geographic space. The unique pattern is the result of complex
spatial processes determining where people live that are driven by a host of
factors—not spurious, arbitrary, constant or even “normal” events.
Now
turn your attention to the numeric distribution of the data depicted in the
right side of the figure. The Data
View was generated by simply transferring the grid values in the
analysis frame to Excel, then applying the Histogram
and Descriptive Statistics options
of the Data Analysis add-in tools. The
map organizes the data as 100 rows by 100 columns (X,Y) while the non-spatial
view simply summarizes the 10,000 values into a set of statistical indices
characterizing the overall central tendency of the data. The mechanics used to plot the histogram and
generate the statistics are a piece-of-cake, but the real challenge is to make
sense of it all.
Note
that the data aren’t distributed as a normal bell-curve, but appear shifted
(termed skewed) to the left. The tallest
spike and the intervals to its left, match the large expanse of grey values in
the map view—frequently occurring low customer density values. If the surface contained a disproportionably
set of high value locations, there would be a spike at the high end of the
histogram. The red line in the histogram
locates the mean (average) value for the numeric distribution. The red line in the 3D map surface shows the
same thing, except its located in the geographic distribution.
The mental exercise linking geographic space with data space is a good one, and
some general points ought to be noted.
First, there isn’t a fixed relationship between the two views of the
data’s distribution (geographic and numeric).
A myriad of geographic patterns can result in the same histogram. That’s because spatial data contains
additional information—where, as well
as what—and the same data summary of
the “what’s” can reflect a multitude of spatial arrangements (“where’s”).
But is the reverse true? Can a given
geographic arrangement result in different data views? Nope, and it’s this relationship that
catapults mapping and geo-query into the arena of mapped data analysis. Traditional analysis techniques assume a
functional form for the frequency distribution (histogram shape), with the
standard normal (bell-shaped) being the most prevalent.
Spatial
statistics, the foundation of geo-business applications, doesn’t predispose any
geographic or numeric functional forms—it simply responds to the inherent
patterns and relationships in a data set.
The next several sections describe some of the surface modeling and
spatial data mining techniques available to the venturesome few who are willing
to work “outside the lines” of traditional mapping and statistics.
_____________________________
Author’s Note: a more detailed treatise and hands-on
exercises in GIS concepts, procedures and applications in business is in the
workbook Analyzing Geo-Business Data (Berry, 2003) available for
download from www.innovativegis.com.
Myriad
Techniques Help to Interpolate Spatial Distributions
(GeoWorld, July 2008)
Statistical
sampling has long been at the core of business research and practice. Traditionally data analysis used non-spatial
statistics to identify the “typical” level of sales, housing prices, customer
income, etc. throughout an entire neighborhood, city or region. Considerable effort was expended to determine
the best single estimate and assess just how good the “average” estimate was in
typifying the extended geographic area.
However
non-spatial techniques fail to make use of the geographic patterns inherent in
the data to refine the estimate—the typical level is assumed everywhere the
same throughout a project area. The
computed variance (or standard deviation) indicates just how good this
assumption is—the larger the standard deviation, the less valid is the assumption
“everywhere the same.” But no information is provided as to where
values might be more or less than the computed typical value (average).
Spatial
Interpolation, on the other hand, utilizes spatial patterns in a
data set to generate localized estimates throughout the sampled area. Conceptually it “maps the variance” by using geographic position to help explain the
differences in the sample values. In
practice, it simply fits a continuous surface (kind of like a blanket) to the
point data spikes (figure 1).
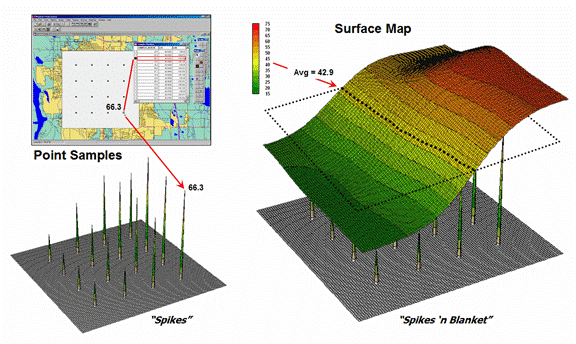
Figure 1. Spatial
interpolation involves fitting a continuous surface to sample points.
While
the extension from non-spatial to spatial statistics is a theoretical leap, the
practical steps are relatively easy. The
left side of figure 1 shows 2D and 3D “point maps” of data samples depicting
the percentage of home equity loan to market value. Note that the samples are geo-referenced
and that the sampling pattern and
intensity are different than those generally used in traditional
non-spatial statistics and tend to be more regularly spaced and numerous.
The surface
map on the right side of figure 1 translates pattern of the “spikes” into the
peaks and valleys of the surface map representing the data’s spatial
distribution. The traditional,
non-spatial approach when mapped is a flat plane (average everywhere) aligned
within the yellow zone. Its “everywhere
the same” assumption fails to recognize the patterns of larger levels (reds)
and smaller levels (greens). A decision
based on the average level (42.88%) would be ideal for the yellow zone but
would likely be inappropriate for most of the project area as the data vary
from 16.8 to 72.4 percent.
The
process of converting point-sampled data into continuous map surfaces
representing a spatial distribution is termed Surface Modeling involving density analysis and map generalization
(discussed last month), as well as spatial interpolation techniques. All spatial interpolation techniques
establish a "roving window" that—
-
moves to a grid location in a project
area (analysis frame),
-
calculates an estimate based on the
point samples around it (roving window),
-
assigns the estimate to the center cell
of the window, and then
-
moves to the next grid location.
The
extent of the window (both size and shape) affects the result, regardless of
the summary technique. In general, a large window capturing a larger
number of values tends to "smooth" the data. A smaller window
tends to result in a "rougher" surface with more abrupt transitions.
Three
factors affect the window's extent: its reach, the number of samples, balancing.
The reach, or search radius, sets a limit on how far the computer
will go in collecting data values. The number of samples
establishes how many data values should be used. If there is more than
the specified number of values within a specified reach, the computer uses just
the closest ones. If there are not enough values, it uses all that it can
find within the reach. Balancing
of the data attempts to eliminate directional bias by ensuring that the values
are selected in all directions around window's center.
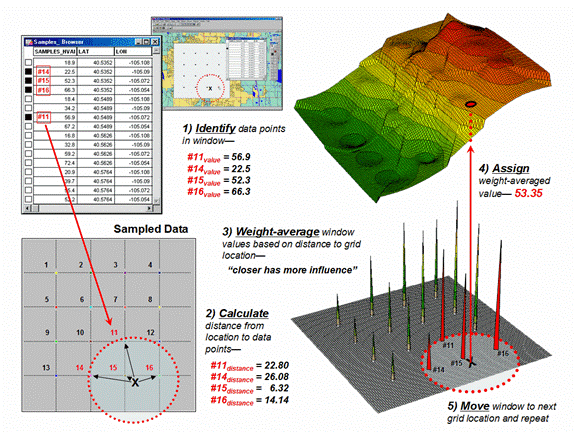
Once a
window is established, one of several summary techniques comes into play. Inverse distance weighted (IDW) is an easy spatial
interpolation technique to conceptualize (see figure 2). It estimates the
value for a location as an average of the data values within its
vicinity. The average is weighted in a manner that decreases the
influence of the surrounding sample values as the distance increases. In
the figure, the estimate of 53.35 is the "inverse distance-squared (1/D2)
weighted average" of the four samples in the window. Sample #15 (the
closest) influences the average a great deal more than sample #14 (farthest
away).
The
right portion of figure 2 contains three-dimensional (3-D) plots of the point
sample data and the inverse distance-squared surface generated. The
estimated value in the example can be conceptualized as "sitting on the
surface," 53.35 units above the base (zero).
Figure 2. Inverse distance weighted interpolation
weight-averages sample values within a roving window.
Figure 3. Example Calculations for Inverse Distance
Squared Interpolation.
Figure
3 shows the weighted average calculations for spatially interpolating the
example location in figure 2. The
Pythagorean Theorem is used to calculate the Distance from the Grid Location to each of the data Samples within the summary window. The distances are converted to Weights that are inversely proportional
(1/D2; see example calculation in the figure). The sample Values are multiplied by their computed Weights and the “sum of the products” is divided by the “sum of the
weights” to calculate the weighted average value (53.35) for the location on
the interpolated surface.
Because
the inverse distance procedure is a fixed, geometric-based method, the
estimated values can never exceed the range of values in the original field
data. Also, IDW tends to "pull-down peaks and pull-up valleys"
in the data, as well as generate “bull’s-eyes” around sampled locations.
The technique is best suited for data sets with samples that exhibit minimal
regional trends.
However,
there are numerous other spatial interpolation techniques that map the spatial
distribution inherent in a data set.
Critical to surface modeling is an ability to benchmark interpolation
results from different techniques and describe a procedure for assessing which
is best (see Author’s Note) …certainly a “must read” for techie-types.
_____________________________
Author’s Note: The
first section of the Further Online Reading listing at the end of this topic
describes the application of residual analysis for “Interpreting Interpolation
Results (and why it is important).”
Use Map
Analysis to Characterize Data Groups
(GeoWorld, September 2008)
One of
the most fundamental techniques in map analysis is the comparison of a set of
maps. This usually involves staring at
some side-by-side map displays and formulating an impression about how the
colorful patterns do and don’t appear to align.
But
just how similar is one location to another?
Really similar, or just a little bit similar? And just how dissimilar are all of the other
areas? While visual (visceral?) analysis
can identify broad relationships, it takes quantitative map analysis to generate
the detailed scrutiny demanded by most Geo-business applications.
Consider
the three maps shown in figure 1— what areas identify similar data
patterns? If you focus your attention on
a location in the southeastern portion, how similar are all of the other
locations? Or how about a northeastern
section? The answers to these questions
are far too complex for visual analysis and certainly beyond the geo-query and
display procedures of standard desktop mapping packages.
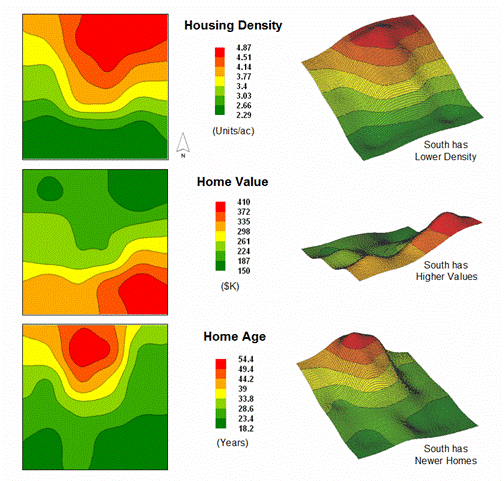
The
mapped data in the example show the geographic patterns of housing density,
value and age for a project area. In
visual analysis you move your focus among the maps to summarize the color
assignments (2D) or relative surface height (3D) at different locations. In the southeastern portion the general
pattern appears to be low Density, high Value and low Age— low, high, low. The northeastern portion appears just the
opposite—high, low, high.
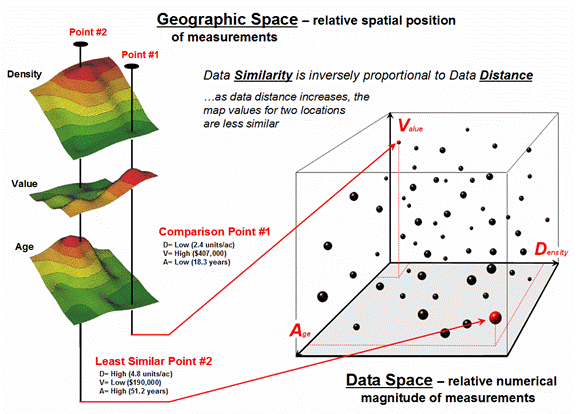
Figure
1. Map surfaces identifying the spatial
distribution of housing density, value and age.
The
difficulty in visual analysis is two-fold— remembering the color patterns and
calculating the difference. Quantitative
map analysis does the same thing except it uses the actual map values in place
of discrete color bands. In addition,
the computer doesn’t tire as easily as you and completes the comparison
throughout an entire map window in a second or two (10,000 grid cells in this
example).
The
upper-left portion of figure 2 illustrates capturing the data patterns for
comparing two map locations. The “data
spear” at Point #1 identifies the housing Density as 2.4 units/ac, Value as
$407,000 and Age as 18.3 years. This step
is analogous to your eye noting a color pattern of green, red, and green. The other speared location at Point #2
locates the least similar data pattern with housing Density of 4.8 units/ac,
Value of $190,000 and Age of 51.2 years— or as your eye sees it, a color
pattern of red, green, red.
Figure
2. Conceptually linking geographic space
and data space.
The
right side of the figure schematically depicts how the computer determines
similarity in the data patterns by analyzing them in three-dimensional “data
space.” Similar data patterns plot close
to one another with increasing distance indicating decreasing similarity. The realization that mapped data can be
expressed in both geographic space and data space is paramount to understanding
how a computer quantitatively analyses numerical relationships among mapped
data.
Geographic space uses
earth coordinates, such as latitude and longitude, to locate things in the real
world. The geographic expression of the
complete set of measurements depicts their spatial distribution in familiar map
form. Data space, on the other hand, is a bit less familiar. While you can’t stroll through data space you
can conceptualize it as a box with a bunch of balls floating within it.
In the
example, the three axes defining the extent of the box correspond to housing
Density (D), Value (V) and Age (A). The
floating balls represent data patterns of the grid cells defining the
geographic space—one “floating ball” (data point) for each grid cell. The data values locating the balls extend
from the data axes—2.4, 407.0 and 18.3 for the comparison point identified in figure 2. The other point has considerably higher
values in D and A with a much lower V values so it plots at a different location
in data space (4.8, 51.2 and 190.0 respectively).
The
bottom line for data space analysis is that the position of a point in data
space identifies its numerical pattern—low, low, low in the back-left corner,
and high, high, high in the upper-right corner of the box. Points that plot in data space close to each
other are similar; those that plot farther away are less similar. Data distance is the way computers “see” what
you see in the map displays. The real
difference in the graphical and quantitative approaches is in the details—the
tireless computer “sees” extremely subtle differences between all of the data
points and can generate a detailed map of similarity.
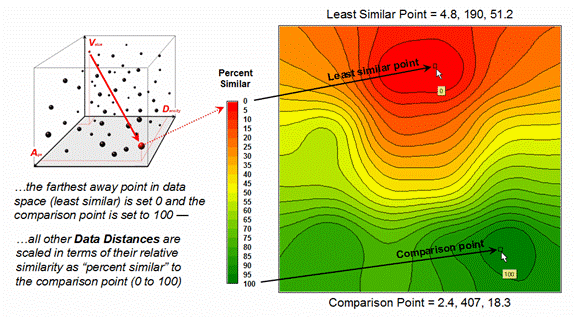
In the
example in figure 2, the floating ball closest to you is least similar—greatest
“data distance” from the comparison point.
This distance becomes the reference for “most different” and sets the
bottom value of the similarity scale (0% similar). A point with an identical data pattern plots
at exactly the same position in data space resulting in a data distance of 0
equating to the highest similarity value (100% similar).
The
similarity map shown in figure 3 applies a consistent scale to the data
distances calculated between the comparison point and all of the other
points. The green tones indicate
locations having fairly similar D, V and A levels to the comparison
location—with the darkest green identifying locations with an identical data
pattern (100% similar). It is
interesting to note that most of the very similar locations are in the southern
portion of the project area. The
light-green to red tones indicate increasingly dissimilar areas occurring in
the northern portion of the project area.
A
similarity map can be an extremely valuable tool for investigating spatial patterns
in a complex set of mapped data. The
similarity calculations can handle any number of input maps, yet humans are
unable to even conceptualize more than three variables (data space box). Also, the different map layers can be
weighted to reflect relative importance in determining overall similarity. For example, housing Value could be specified
as ten times more important in assessing similarity. The result would be a different map than the
one shown in figure 3— how different depends on the unique coincidence and
weighting of the data patterns themselves.
Figure
3. A similarity map identifies how
related locations are to a given point.
In
effect, a similarity map replaces a lot of general impressions and subjective
suggestions for comparing maps with an objective similarity measure assigned to
each map location. The technique moves
map analysis well beyond traditional visual/visceral map interpretation by
transforming digital map values into to a quantitative/consistent index of
percent similarity. Just click on a
location and up pops a map that shows how similar every other location is to
the data pattern at the comparison point— an unbiased appraisal of similarity.
_____________________________
Author’s Note: a more detailed treatise and hands-on
exercises in GIS concepts, procedures and applications in business is in the
workbook Analyzing Geo-Business Data (Berry, 2003) available for
download from www.innovativegis.com.).
Discover
the “Miracles” in Mapping Data Clusters
(GeoWorld, November 2008)
The last
couple of sections have focused on analyzing data similarities within a stack
of maps. The first technique, termed Map
Similarity, generates a map showing how similar all other areas are to a
selected location. A user simply clicks
on an area and all of the other map locations are assigned a value from zero
(0% similar—as different as you can get) to one hundred (100% similar—exactly
the same data pattern).
The
other technique, Level Slicing, enables a user to specify a data range
of interest for each map layer in the stack then generate a map identifying the
locations meeting the criteria. Level
Slice output identifies combinations of the criteria met—from only one
criterion (and which one it is), to those locations where all of the criteria
are met.
While
both of these techniques are useful in examining spatial relationships, they
require the user to specify data analysis parameters. But what if you don’t know which locations in
a project area warrant Map Similarity investigation or what Level Slice
intervals to use? Can the computer on
its own identify groups of similar data?
How would such a classification work?
How well would it work?
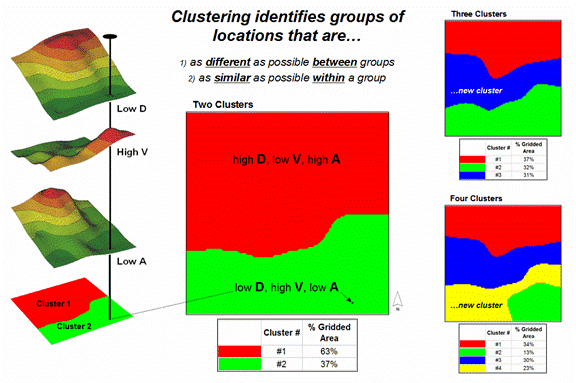
Figure
1. Example output from map clustering.
Figure
1 shows some example spatial patterns derived from Map Clustering. The
“floating” map layers on the left show the input map stack used for the cluster
analysis. The maps are the same ones
used in previous examples and identify the geographic and numeric distributions
of housing Density, home Value and home Age levels throughout the example
project area.
The map
in the center of the figure shows the results of classifying the D, V and A map
stack into two clusters. The data
pattern for each cell location is used to partition the field into two groups
that are 1) as different as possible between groups and 2)
as similar as possible within a group. If all went well, any other division of the
mapped data into two groups would be worse at mathematically balancing the two
criteria.
The two
smaller maps on the right show the division of the data set into three and four
clusters. In all three of the cluster
maps, red is assigned to the cluster with relatively high Density, low Value
and high Age responses (less wealthy) and green to the one with the most
opposite conditions (wealthy areas).
Note the encroachment at the margin on these basic groups by the added
clusters that are formed by reassigning data patterns at the classification
boundaries. The procedure is effectively
dividing the project area into “data neighborhoods” based on relative D, V and
A values throughout the map area.
Whereas traditional neighborhoods usually are established by historical
legacy, cluster partitions respond to similarity of mapped data values and can
be useful in establishing insurance zones, sales areas and marketing clusters.
The
mechanics of generating cluster maps are quite simple. Just specify the input maps and the number of
clusters you want then miraculously a map appears with discrete data
groupings. So how is this miracle performed? What happens inside clustering’s black box?
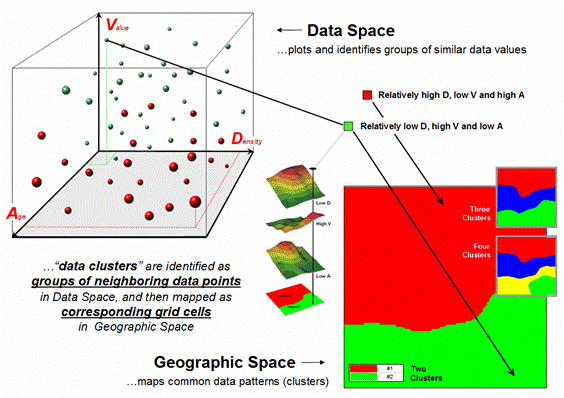
The
schematic in figure 2 depicts the process.
The floating balls identify the data pattern for each map location (in
Geographic Space) plotted against the P, K and N axes (in Data Space). For example, the tiny green ball in the
upper-right corner corresponds to a map location in the wealthiest part of town
(low D, high V and low A). The large red
ball appearing closest depicts a location in a less wealthy part (high D, low V
and high A). It seems sensible that
these two extreme responses would belong to different data groupings (clusters
1 and 2, respectively).
While
the specific algorithm used in clustering is beyond the scope of this
discussion (see author’s note), it suffices to recognize that data distances
between the floating balls are used to identify cluster membership— groups of
balls that are relatively far from other groups (different between groups) and
relatively close to each other (similar within a group) form separate data
clusters. In this example, the red balls
identify relatively less wealthy locations while green ones identify wealthier
locations. The geographic pattern of the
classification (wealthier in the south) is shown in the 2D maps in the lower
right portion of the figure.
Identifying
groups of neighboring data points to form clusters can be tricky business. Ideally, the clusters will form distinct
“clouds” in data space. But that rarely
happens and the clustering technique has to enforce decision rules that slice a
boundary between nearly identical responses.
Also, extended techniques can be used to impose weighted boundaries
based on data trends or expert knowledge.
Treatment of categorical data and leveraging spatial autocorrelation are
additional considerations.
Figure
2. Data patterns for map locations are
depicted as floating balls in data space with groups of nearby patterns
identifying data clusters.
So how
do know if the clustering results are acceptable? Most statisticians would respond, “…you can’t
tell for sure.” While there are some
elaborate procedures focusing on the cluster assignments at the boundaries, the
most frequently used benchmarks use standard statistical indices, such as T-
and F-statistics used in comparing sample populations.
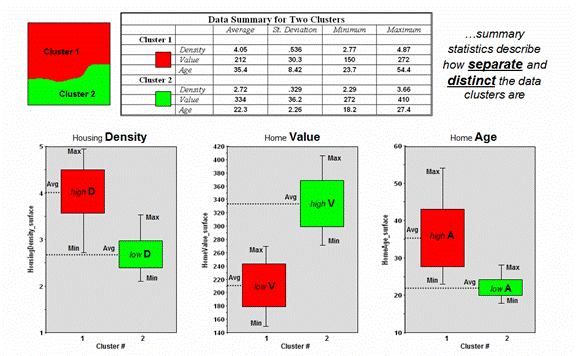
Figure
3 shows the performance table and box-and-whisker plots for the map containing
two data clusters. The average, standard
deviation, minimum and maximum values within each cluster are calculated. Ideally the averages between the two clusters
would be radically different and the standard deviations small—large difference
between groups and small differences within groups.
Box-and-whisker
plots enable us to visualize these differences.
The box is aligned on the Average (center of the box) and extends above
and below one Standard Deviation (height of the box) with the whiskers drawn to
the minimum and maximum values to provide a visual sense of the data range. If the plots tend to overlap a great deal, it
suggests that the clusters are not very distinct and indicates significant
overlapping of data patterns between clusters.
Figure
3. Clustering results can be evaluated
using “box and whisker” diagrams and basic statistics.
The
separation between the boxes in all three of the data layers of the example
suggests good distinction between the two clusters with the Home Value grouping
the best with even the Min/Max whiskers not overlapping. Given the results, it appears that the
clustering classification in the example is acceptable… and hopefully the statisticians
among us will accept in advance my apologies for such an introductory and
visual treatment of a complex topic.
_____________________________
Author’s Note: The clustering algorithm used in the
examples was described in Beyond Mapping Compilation Series, book III, Topic
10, Further Reading section 4, “Identify Data Patterns.” Related discussion and hands-on exercises on
Clustering are in Topic 7, “Spatial Data Mining” in the workbook Analyzing
Geo-Business Data (Berry, 2003) available for download from www.innovativegis.com.
The
Universal Key for Unlocking GIS’s Full Potential
(GeoWorld, October 2011)
Geotechnology is rapidly changing
how we perceive, process and provide spatial information. It is generally expected that one can click
anywhere in the world and instantly access images and basic information about a
location. However, accessing your own
specialized and proprietary data is much more difficult—often requiring
wholesale changes to your corporate database and staffing.
The emergence of Geo-Web
Applications involving the integration/interaction of GIS, visualization and
social media has set the stage for entirely new perspectives on corporate
DBMS. For example, one can upload sales
figures for individual customers into Google Earth and view as clusters of pins
draped on an aerial image of a city, or receive GPS-tagged photos of potholes
on county roads, or track shipments and field crews, or even locate vacant
parking spaces at the mall—all this and more from your somewhat overly-smart
cell phone.
Generally speaking there
are three information processing modes…
-
Visualize— to recall or form
mental images or pictures involving map display (Charting capabilities),
-
Synthesize— to form a material
or abstract entity by combining parts or elements involving the
re-packaging of existing information (Geo-query capabilities), and
-
Analyze— to separate a
material or abstract entity into constituent parts or elements to
determine their relationship involving deviation of new spatial
information identifying key factors, connections and
associations (Map Analysis capabilities).
Map Analysis is by far
the least developed of the three.
Visualization and query of mapped data are direct extensions of our
paper map and filing systems legacy.
Analysis of mapped data, on the other hand, involves somewhat unfamiliar
territory for most organizations. Like
“the chicken and the egg” quandary, the demand for map analysis hasn’t been
there because prior experience with map analysis hasn’t been there. But even more basic is the lack of mapped
data in a form amenable for analysis.
Your grade school
exposure to geography and mapping can change all that. Recall that Latitude (north/south) and
Longitude (east/west) lines can be drawn on the globe to identify a
location anywhere in the world. Using
typical single precision floating point storage of Lat/Long coordinates in a
standard database enables grid cell referencing of about half a foot or less
anywhere in the continental U.S. (365214 ft/degree * 0.000001= .365214 ft
*12 = 4.38257 inch grid precision
along the equator). That means appending Lat/Long
fields to any database record locates that record with more than enough
precision for most map analysis applications.
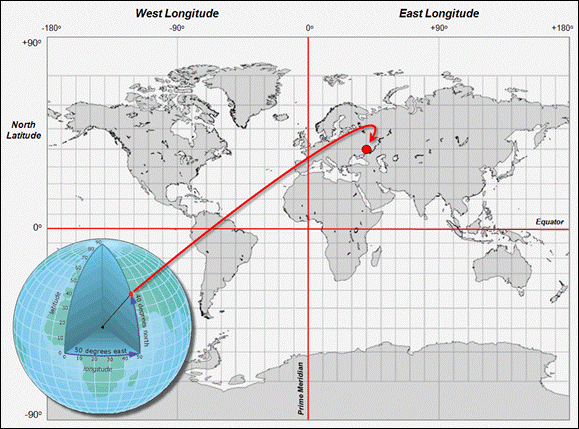
As review, recall that
the Lat/Long coordinate system uses solid angles measured from the center of
the earth (figure 1). A line passing
through the Royal Observatory in Greenwich near London (termed the Prime
Meridian) serves as the international zero-longitude reference. Locations to the east are in the eastern
hemisphere, and places to the west are in the western hemisphere with each half
divided into 180 degrees.
Geographic latitude
measures the angle from the equator to the poles that trace circles on the
Earth’s surface called parallels, as they are parallel to the equator and to
each other. The equator divides the
globe into Northern and Southern Hemispheres— 0 to 90° North and 0 to 90°
South. Figure 1 shows a ten degree
Lat/Long gridding steps representing approximately 692 mile movements along the
equator.
Figure 1. The Latitude/Longitude coordinate system
forms a comprehensive grid covering the entire world with cells of about half a
foot or less over the continental U.S.
So much
for a conceptual review of Lat/Long, keeping in mind that there are lot of
geographic and mathematical considerations in implementing the coordinate
system. Thankfully they were
hammered-out years ago resulting in a set universal standards that form the
foundation for contemporary GPS use.
The next conceptual step
involves extending the paper map paradigm to grid-based data layers. Traditional mapping holds that there are
three fundamental map features— discrete points, lines and polygons. With the advent of the digital map, a fourth
feature type emerges—continuous surfaces. The Lat/Long grid forms a surface for
geographic referencing that is analogous to a digital image with a “dot”
(pixel) for every location in viewed area.
In the case of a grid map layer, a map value that identifies the
characteristic/condition at a location replaces the pixel value denoting color.
Like the image on a computer
screen, a point feature is represented by a single dot/cell containing that
feature; a line feature by a series of connected cells; and a polygon feature
by all of the cells defining it, both its interior and boundary. A surface is represented by the entire
gridded continuum and like an elevation surface it depicts continuous changes
in a map variable. Whereas points, lines
and polygons have sharp abrupt boundaries, surfaces form gradients of change.
Figure 2. The Lat/Long grids are used to construct a
map stack of geo-registered map layers that are pre-conditioned for map
analysis and modeling.
The final conceptual leap
is shown in figure 2. Like Google
Earth’s registration of satellite images to Lat/Long referencing, mapped data
of all types can be stored, retrieved and analyzed based on the stored
coordinates for the records—thereby forming a “Universal DBMS Key” that
can link seemingly disparate database files.
The process is similar to a date/time stamp, except the “where
information” provides a spatial context for joining data sets. Demographic records can be linked to resource
records that in turn can be linked to business records, etc.
In practice, extensive
data is stored in “Virtual Tiles” for efficient storage, access and
processing. A user identifies a boundary
extent, then an “Analysis Frame” resolution (cell size) and
pertinent data layers that are automatically extracted into a “Map Stack”
for grid-based map analysis and modeling.
Solution map(s) resulting from analysis can be exported in either
vector, raster or DBMS form and the map stack retained for subsequent
processing or deleted and reconstructed as needed.
So what is holding back
this seemingly utopian mapping world?
The short answer is “some practical and legacy considerations.” On the practical front, the geographic
stretching and pinching of the grid cells with increasing latitude confounds map
analysis at global scales and lacks the precision necessary for detailed
cadastral/surveying applications. On the
legacy front, the approach relies more on DBMS and image processing mindsets
than on traditional mapping paradigms and geographic principles underlying most
flagship GIS packages.
It is like a Rorschach
inkblot. Since the middle ages we have
thought of Lat/Long as intersecting lines, whereas the new perspective
is flipped to a continuum of grid cells.
Current thinking is more like a worldwide egg crate with the grid spaces
as locations for placing map values that indicate the
characteristics/conditions of a multitude of map variables anywhere in the
world.
As the Geo-Web mindset
gains acceptance and data storage becomes ubiquitous, more and more maps will
take on image characteristics—a raster map where Lat/Long grid cells replace
pixels and map values amenable to analysis replace color codes. While the vector map model will continue, it
is the raster model (Lat/Long grids in particular) that takes us well beyond
traditional mapping.
_____________________________
Author’s Notes: For
more information on grid-based mapped data considerations, see Beyond Mapping
Compilation Series, book IV, Topic 1 “Extending Grid-based Data Concepts” posted
at www.innovativegis.com.
_____________________
Further Online Reading: (Chronological listing posted at www.innovativegis.com/basis/BeyondMappingSeries/)
Interpreting Interpolation Results (and why
it is important) — describes the use of “residual analysis” for
evaluating spatial interpolation performance (August 2008)
Get “Map-ematical” to Identify Data Zones
— describes the use of “level-slicing” for classifying locations with a
specified data pattern (October 2008)
Can We Really Map the Future? — describes
the use of “linear regression” to develop prediction equations relating
dependent and independent map variables (December 2008)
Follow These Steps to Map Potential Sales
— describes an extensive geo-business application that combines
retail competition analysis and product sales prediction (January 2009)