|
Topic 5 –
Calculating Visual Exposure |
Map
Analysis book/CD |
Line-of-Sight
Buffers Add Intelligent to Maps — describes
procedures for creating buffers that track relative visual exposure and noise
levels
Identify
and Use Visual Exposure to Create Viewshed Maps — discusses basic
considerations and procedures for establishing visual connectivity
Visual
Exposure is in the Eye of the Beholder — describes procedures for
assessing visual impact and creating simple models
Use
Exposure Maps and Fat Buttons to Assess Visual Impact
— investigates procedures for assessing visual exposure
Further Reading
— two additional sections
<Click here>
for a printer-friendly version of this
topic (.pdf).
(Back to the Table of Contents)
______________________________
Line-of-Sight
Buffers Add Intelligent to Maps
(GeoWorld, December 2000)
As
noted in the earlier discussions of proximity, simple buffers are
often just that— too simple for real world applications. The assumption that there are uniform
conditions throughout a fixed distance from a map feature rarely squares with
reality. A consistent 100, 200 or
300-meter buffer around roads often includes inappropriate results within a
buffer, such as ocean areas. Or they can
include areas that are inconsistent with an assumption, such as a concern for
just the uphill locations from roads.
Variable-width
buffers,
on the other hand, respond to both intervening conditions and the type of
connectivity. They expand and contract
to reflect spatial reality around map features by clipping inappropriate and
inconsistent areas.
Tracking
the variations within a buffer is just as important. Instead of simply being within or outside a
buffered area, each location can be identified as to its proximity to the
buffered feature. For example, all of
the uphill locations within 250 meters (variable-width buffer) can be assigned
their proximity to a road—a continuum of information throughout the buffer
instead of simply an “in or out” characterization.
Another
type of variable-width buffer involves line-of-sight connectivity. In this application a viewer location
“looks” over an elevation surface up to a specified distance and identifies all
of the areas it can see.
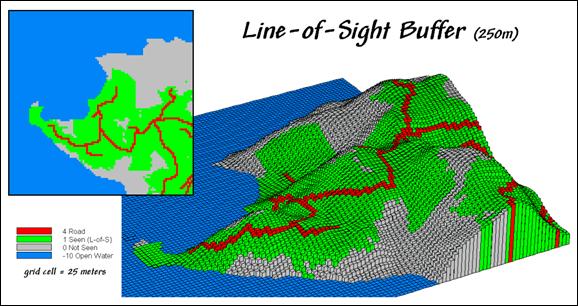
Figure
1. The “viewshed” of the road network
forms a variable-width, line-of-sight buffer.
Figure
1 shows a 250-meter line-of-sight buffer surrounding the road
network. Note that variations in the
terrain cause the buffer to truncate areas that are not seen, yet are still
within the 250-meter reach.
The conceptual
basis for calculating line-of-sight connectivity is quite simple. The position of a viewer location (one of the
road cells in this example) determines its height from an elevation map of the
area. The cell’s height is compared to
the elevations of its eight surrounding cells to establish a set of rise-to-run
ratios—change in elevation per horizontal distance. The rise/run ratios for the next ring of
cells are computed. If a new location’s
ratio is greater, it is marked as seen and its ratio becomes the one to beat
for subsequent locations in that direction.
The process is repeated for successive rings up to the buffer
limit. Then the next viewer cell is
considered until the entire road network has been evaluated.
In
practice, the line-of-sight procedure is a bit more complex as additional
factors, such as vegetation height, often are included in determining the viewshed
defining the buffered area. Also, the
process can be extended to keep track of the number of times each buffer
location is seen (e.g., number of road cells connected to it). The result is a measure of visual exposure
for each buffer location. Instead of
simply delineating the buffer limits, information about the relative exposure
throughout the buffer is noted.
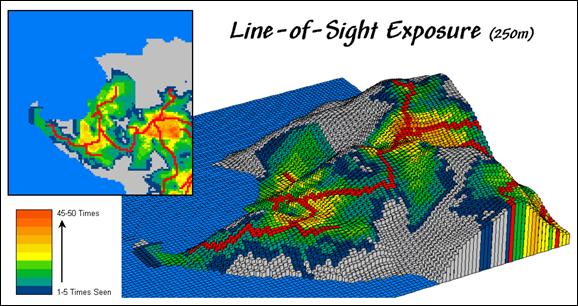
Figure
2. A “visual exposure” map identifies
the number of times each map location is visually connected to an extended map
feature.
Figure
2 contains a map of the visual exposure within the 250-meter viewshed. Note the four areas of relatively high
exposure to roads (warmer tones). While
these areas might be ideal for visually aesthetic activities, the areas of
minimal exposure (cool tones) or those entirely outside the buffer (gray) are
more suitable for “ugly things.” For
example, a national park might use a visual exposure buffer to assist forest
planning for foreground management zones.
A telecom company might use the information to help locate
cell-towers.
Or a
developer might focus on candidate areas for “Tranquil Acres Estates” that have
minimal visual exposure and road noise.
Spatial modeling of noise dissipation can be a complex undertaking, but
line-of-sight connectivity is a fundamental element. While sound waves bend more than light waves,
they also tend to be blocked by intervening terrain. A road location on the other side of a ridge
is neither seen nor heard—provided there is a big pile of dirt separating the
source and receptor.
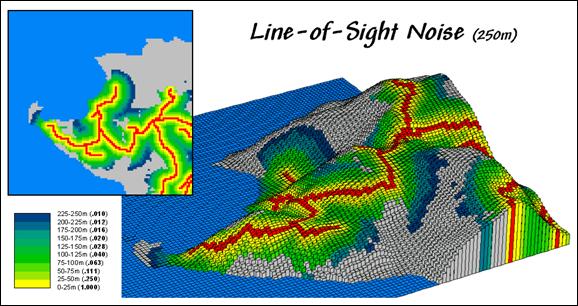
Also,
sound waves fade dramatically as a function of distance (1/d2). Figure 3 incorporates this dissipation for a
line-of-sight noise buffer.
The cells adjacent to the road are the loudest (yellow—1.00 times the
noise level). Those at the limit of the
250-meter reach are a whole lot quieter (blue—0.010 times the noise
level). Noise levels at cells that have
intervening terrain or are beyond the buffer-reach (gray) are considered
inaudible.
Figure
3. A simple “noise buffer” model
considers distance-falloff as well as line-of-sight connectivity.
Admittedly,
the assumptions in modeling noise dissipation in this example are simplified
(see Author’s Note), but they do reflect reality better than a simple buffer
that totally ignores the very real effects of distance and surrounding
terrain. There are several possibilities
for improving the accuracy of the noise levels within the buffer, such as
treating neighboring vegetation types differently. However, these extensions involve
consideration of “relative barriers” in characterizing variable-width
buffers—the topic for next month’s column.
_______________________
Author's Note: for more discussion on noise analysis and
abatement modeling, see www.nonoise.org/library/highway/policy.htm.
Identify
and Use Visual Exposure to Create Viewshed Maps
(GeoWorld, June 2001)
Several
earlier discussions have discussed the concept of effective proximity in
deriving variable width buffers and travel-time movement. The procedures relax the assumption that
distance is only measured as “the shortest straight line between two
points.” Real world movement is rarely
straight as it responds to a complex set of absolute and relative barriers. While the concept of effective proximity
makes common sense, its practical expression had to wait for
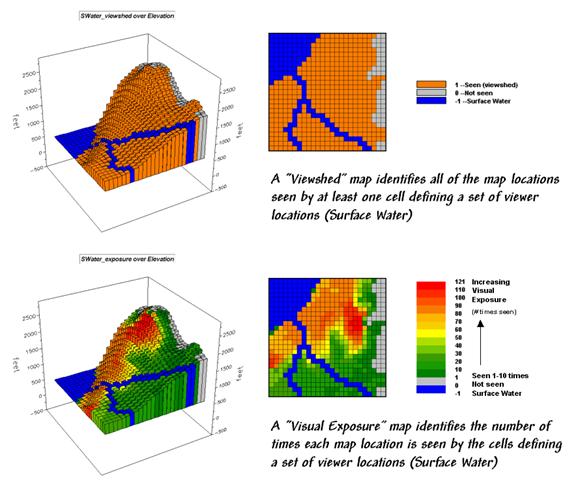
Figure
1. Viewshed of all surface water locations.
Similarly,
the measurement of visual connectivity as outlined in the previous
section is relatively new to map analysis but has always been part of a
holistic perspective of a landscape. We
might not be able to manually draw visual exposure surfaces yet the idea of
noting how often locations are seen from other areas is an important ingredient
in realistic planning. Within a
For
example, the viewshed map shown in top portion of figure 1
identifies all the map locations that are seen (tan) by at least one cell of
surface water (dark blue). The light
gray locations along the right side of the map locate areas that are not
visually connected to water—bum places for hikers wanting a good view of
surface water while enjoying the scenery.
The
bottom portion of the figure takes visual connectivity a step further by
calculating the number of times each map location is seen by the “viewer”
cells. In the example there are 127
water cells and one location near the top of the mountain sees 121 of them…
very high visual exposure to water. In effect, the exposure surface “paints” the
viewshed by the relative amount of exposure—green not much and red a whole lot.
So how
does the computer determine visual connectivity? The procedure actually is quite simple (for a
tireless computer) and is similar to the calculation of effective
proximity. A series of “distance waves”
radiate out from a water cell like the ripples from a rock tossed into a pond
(see figure 2).
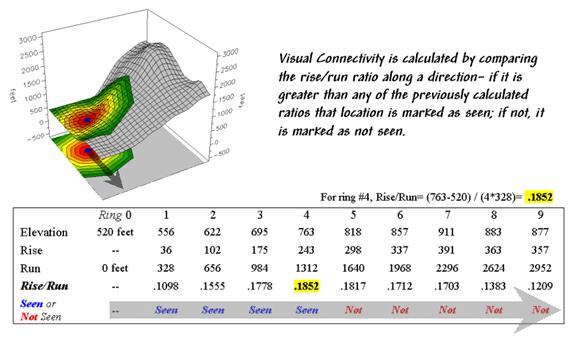
Figure
2. Example calculations for determining
visual connectivity.
As the
wave propagates, the distance from the viewer cell (termed the run) and
the difference in elevation (termed the rise) are calculated for the
cells forming the concentric ring of a wave.
If the rise/run ratio is greater than any of the ratios for the
previous rings along a line from the viewer cell, that location is marked as
seen. If it is smaller, the location is
marked as not seen.
In the
example shown in figure 2, the rise/run ratios to the south (arrow in the
figure) are successively larger for rings 1 through 4 (marked as seen)
but not for rings 5 through 9 (marked as not seen). The computer does calculations for all
directions from the viewer cell and marks the” seen” locations with a value of
one.
The
process is repeated for all of the viewer cells defining surface water
locations—127 times, once for each water cell.
Locations marked with a one identify areas that are seen at least once
and characterize the viewshed of the viewer point. Visual exposure, on the other hand, simply
sums the markers for the number of times each location is seen.
Now
let’s complicate matters a bit. Suppose
there is a dense forest with 75-foot trees that grow like “chia pet” hairs out
of the elevation surface. The forest
canopy height is analogous to raising the elevation surface an equal
amount. But unless you’re a bird, your
eyeball stays on the ground and the trees act like screens blocking your
view.
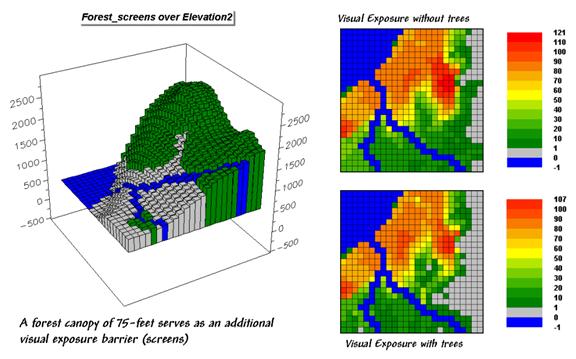
Figure
3. Introducing visual screens that block
line-of-sight connections.
The 3-D
plot in figure 3 shows the effect of introducing a 75-foot forest canopy onto
the elevation surface. Note the sharp walls
around the water cells, particularly in the lower right corner. The view on the ground from these areas is
effectively blocked. The computer
“knows” this because the first ring’s rise/run ratio is very large (big rise
for a small run) and is nearly impossible to beat in subsequent rings.
The
consequence of the forest screens is shown in the maps on the right. The top one doesn’t consider trees, while the
bottom one does. Note the big increase
in the “not seen” area (gray) along the stream in the lower right where the
trees serve as an effective visual barrier.
If your motive is to hide something ugly in these areas from a hiking
trail along the stream, the adjacent tree canopy is extremely important.
The
ability to calculate visual connectivity has many applications. Resource managers can determine the visual
impact of a proposed activity on a scenic highway. County planners can assess what is seen, and
who in turn can see, a potential development.
Telecommunication engineers can try different tower locations to “see”
which residences and roadways are within the different service areas.
Within
a
Visual Exposure is in the Eye of the Beholder
(GeoWorld, July 2001)
The
previous section introduced some basic calculations and considerations in
deriving visual exposure. An important notion
was that “viewer” locations can be a point, group of points, lines or areas—any
set of grid cells. In the example
described last month, all of the stream and lake cells were evaluated to
identify locations seen by at least one water cell (termed a viewshed)
or the number of water cells seeing each map location (termed visual
exposure).
In
effect, the water features are similar to the composite eye of a fly with each
grid cell serving as an individual lens.
The resulting map simply reports the line-of-sight connections from each
lens (grid cell) to all of the other locations in a project area.
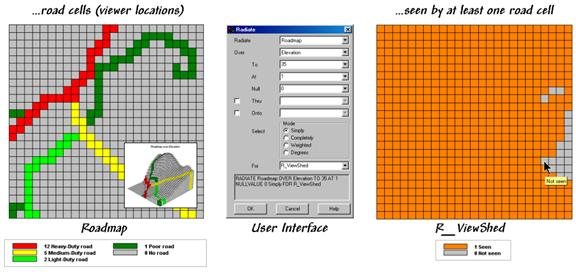
Figure
1 shows a similar analysis for a road network.
The cells defining the roads are shown in the map on the left with a
draped display on the elevation surface as the inset. The computer “goes” to one of the road cells,
“looks” everywhere over the terrain and “marks” each map location that can be
seen with a value of one. The process is
repeated for all of the other road cells resulting in the map on the right—a
viewshed map with seen (tan), not seen (gray).
Figure
1. Identifying the “viewshed” of the
road network.
The interface
in the middle of figure 1 shows how a user coerces the computer to generate a
viewshed map. In the example, the
command Radiate is specified and the Roadmap is selected to
identify the viewer cells. The Elevation
map is selected as the terrain surface whose ridges and valleys determine
visual connectivity from each lens of the elongated eyeball. The To 35 parameter tells the computer
to look up to 35 cells away in all directions— effectively everywhere on the
25x25 cell project area. The At 1
specification indicates that the eyeball is 1-foot over the elevation surface
and the Null 0 sets zero as the background (not a viewer cell). The Thru and Onto
specifications will be discussed a little later.
As the
newer generations of
Locations
on the R_ViewShed map that didn’t receive any connectivity marks (value
0) are not seen from any road cell.
Figure 2 shows results using different calculation modes and the
resulting maps.
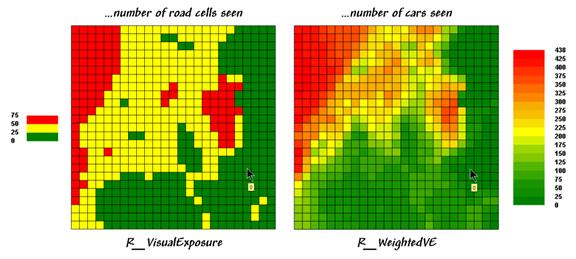
The
values on the R_VisualExposure map were generated by clicking Completely
to calculate the number of roads cells that “see” each location in the project
area—from 0 (not seen) to 75 times seen.
Generally speaking, you put ugly things where the numbers are low and
pretty things where the numbers are high.
But
just the sum of road cells that are visually connected doesn’t always tell the
whole story. Note the values defining
the different types of roads on the Roadmap in figure 1—1 Poor road, 2
Light-duty, 5 Medium-duty, and 12 Heavy-duty.
The values were craftily assigned as “relative weights” indicating the
average number of cars within a 15-minute time period. It’s common sense that a road with more cars
should have more influence in determining visual exposure than one with just a
few cars.
Figure
2. Calculating simple and weighted
visual exposure.
The
calculation mode was switched to Weighted to generate the R_WeightedVE
map displayed on the right side of figure 2.
In this instance, the Roadmap values are summed for each map location
instead of just counting how many road cells are visually connected. The resultant values indicate the relative
visual exposure based on the traffic densities—viewer cells with a lot of cars
having greater influence.
Now
turn your attention to the Thru and Onto specifications in the
example interface. The Thru
hot-field allows the user to specify a map identifying the height of visual
barriers within the area. In last
month’s discussions it was used to place the 50-foot tree canopy for forested
areas—the “chia pet” hairs on top of the elevation surface that blocks visual
connections. The Thru map
contains height values for all “screen” locations and effectively adds the
blocking heights to the elevation values at each location—0 indicates no screen
and 50 indicates a 50-foot visual barrier on top of the terrain.
The Onto
hot-field is conceptually similar but has an important difference. It addresses tall objects, such as smoke-stacks
or towers that might be visible but not wide enough to block views. In this instance, the computer adds the
“target” height when visual connectivity is being considered for a cell
containing a structure but the added height isn’t considered for locations
beyond. The effect is that the feature
pops-up to see if it is seen but doesn’t hang around to block the view beyond
it.
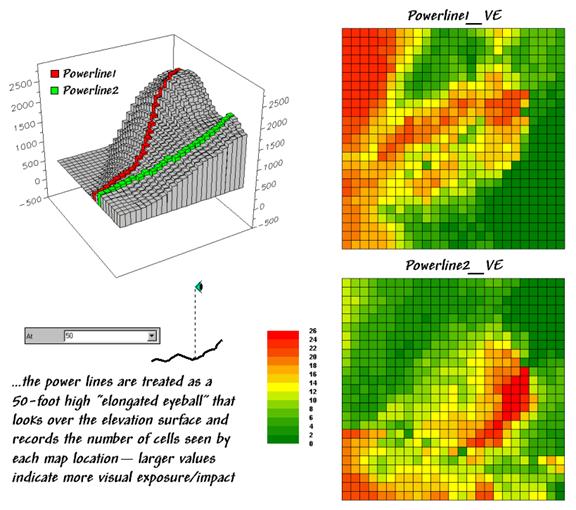
Figure
3. Determining the visual
exposure/impact of alternative power line routes.
Figure
3 depicts yet another way of dealing with extended features. Assume you want to assess the difference in
visual impact of two proposed power line routes shown in the 3-D inset in the
figure. In this instance, Powerline1
is first selected as the viewer map (instead of Roadmap) and the At
parameter is set to 50. The command is
repeated for Powerline2.
These
entries identify the power line cells and their height above the ground. The Powerline1_VE map shows the number
of times each map location is seen by the elongated Powerline1
eyeball. And by “line-of-sight,” if the
power line can see you, you can see the power line. The differences in the patterns between Powerline1_Ve
and Powerline2_VE maps characterize the disparity in visual impact for
the two routes.
What if
your house was in a red area on one and a green area on another? Which route would you favor? … not in my
visual backyard. Next month we’ll
investigate a bit more into how models using visual exposure can be used in
decision-making.
Use Exposure Maps and Fat Buttons to Assess Visual Impact
(GeoWorld, August 2001)
The
last section described several considerations in deriving visual exposure
maps. Approaches ranged from a simple viewshed
(locations seen) and visual exposure (number of times seen) to weighted
visual exposure (relative importance of visual connections). Extended settings discussed included distance,
viewer height, visual barrier height and special object height.
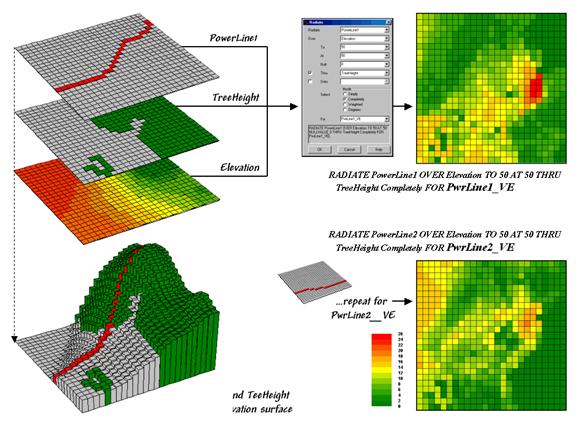
Figure 1. Calculating visual exposure for two proposed
power lines.
Figure
1 rekindles the important points before tackling visual impact modeling. The maps on the left identify input
information for calculating visual exposure.
The PowerLine1 map serves as an elongated eyeball, the TreeHeight
map identifies areas with a 75-foot forest canopy that grows like “chia pet”
hairs on the Elevation surface.
The 3-D
inset is a composite display of all three input maps. The user interface shown in the middle is
used to specify viewer height (At 50)
that raises the power line 50-feet above the surface. A large distance value (To 50) is
entered to force the calculations for all locations in the study area. Finally, the visual exposure mode is
indicated (Completely) and a name assigned to the derived map (PwrLine1_VE).
The
top-left map shows the result with red tones indicating higher visual
exposure. The lower-left map shows
visual exposure for a second proposed power line that runs a bit more to the
south. It was calculated by simply
changing the viewer map to PowerLine2 and the output map to PwrLine2_VE. Compare the patterns of visual exposure in
the two resultant maps. Where do they
have similar exposure levels? Where do
they differ? Which one affects the local
residents more?
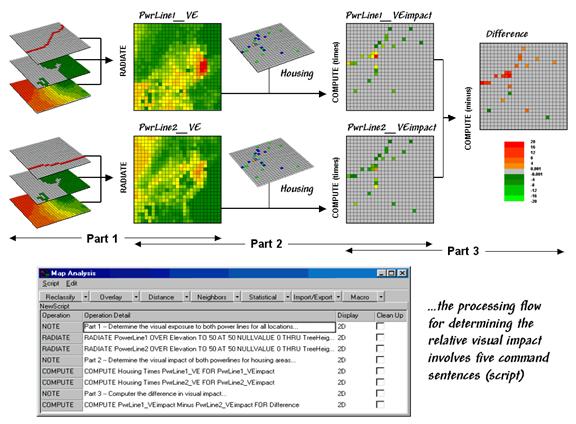
This
final question requires a bit more processing to nail down—locating the
residential areas, “masking” their visual exposure and comparing the results. Figure 2 outlines a simple impact model for
determining the exposure difference between the two proposed routes. The visual exposure maps on the left are the
same as those in figure 1 and serve as the starting point for the impact
model.
The Housing
map identifies grid cells that contain at least one house. The values in the housing cells indicate how
many residences occur in each cell—1 to 5 houses in this case; a 0 value
indicates that no houses are present.
This map is multiplied by the visual exposure maps to calculate the
visual impact for both proposed routes (PwrLine1_VEimpact and PwrLine2_VEimpact). Note that exposure for areas without a house
result in zero impact—0 times any exposure level is 0. Locations with one house report the calculated
exposure level—1 times any exposure level is the same exposure level. Locations with more than one house serve as a
multiplier of exposure impact—2 times any exposure level is twice the impact.
The
final step involves comparing the two visual impact maps by simply subtracting
them. The red tones on the Difference
map identify residential locations that are impacted more by the PowerLine1
route—the higher the value, the greater the difference in impact.
The
dark red locations identify residents that are significantly more affected by
route 1—expect a lot of concern about the route. On the other hand, there are only three
locations that are slightly more affected by route 2 (dark green; fairly low
values).
Figure
2. Determining visual impact on local
residents.
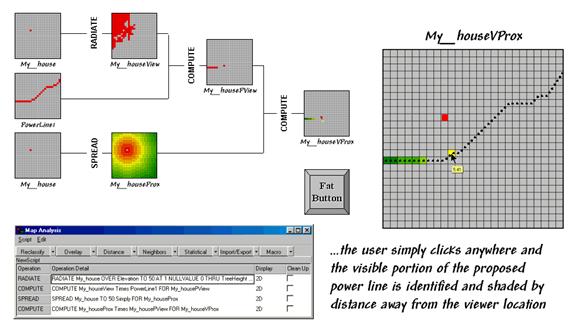
The
information in the lower portion of figure 2 is critical in understanding
The
ability to save and re-run a map analysis sequence sets the stage for the
current revolution in
The
flowchart shows the logical structure of the analysis and the intermediate maps
generated—
-
Calculate the viewshed from the selected
point
-
Mask the portion of the route within the
viewshed
-
Calculate proximity from the selected
point
-
Mask the proximity for just the
proportion of the route
The
script identifies the four sentences that solve the spatial problem. The revolution is represented by the “Fat
Button” in the figure.
Figure
3. Determining visible portions of a proposed
power line.
Within
a
The ability to pop-up special input interfaces and launch command scripts moves
the paradigm of a “
_____________________
Further Online
Reading: (Chronological
listing posted at www.innovativegis.com/basis/BeyondMappingSeries/)
(Extended Visual Exposure Techniques)
Use Maps to Assess Visual
Vulnerability — discusses a procedure for identifying visually
vulnerable areas (February 2003)
Try Vulnerability Maps to Visualize
Aesthetics — describes a procedure for deriving an aesthetics map
based on visual exposure to pretty and ugly places (March 2003)
(Back
to the Table of Contents)