|
Topic 2 –
Fundamental Map Analysis Approaches |
Map
Analysis book/CD |
Moving
Mapping to Analysis of Mapped Data — describes Spatial Analysis and
Spatial Statistics as extensions to traditional mapping and statistics
Bending
Our Understanding of Distance — uses effective distance in
establishing erosion setback to demonstrate spatial analysis
Use
Spatial Statistics to Map Abnormal Averages — discusses surface
modeling to characterize the spatial distribution inherent in a data set
Making
Space for Mapped Data — investigates the link between geographic
space and data space for mapping data patterns
Further Reading
— one additional section
<Click here>
for a printer-friendly version of this
topic (.pdf).
(Back to the Table of Contents)
______________________________
Moving Mapping to Analysis of Mapped Data
(GeoWorld, December 2004)
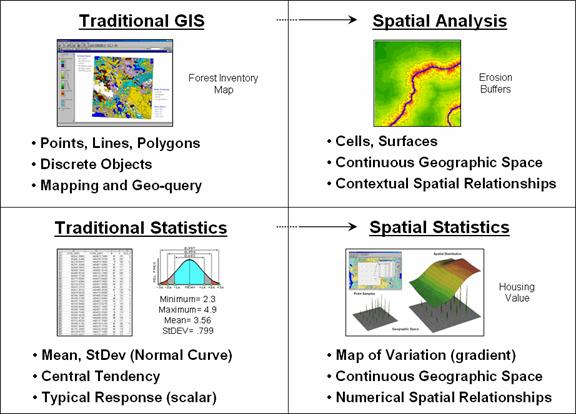
The
evolution (or is it revolution?) of
Figure
1 identifies two key trends in the movement from mapping to map analysis. Traditional
Spatial
Analysis
extends the basic set of discrete map features of points, lines and polygons to
surfaces that represent continuous geographic space as a set of contiguous grid
cells. The consistency of this
grid-based structuring provides a wealth of new analytical tools for
characterizing “contextual spatial relationships”, such as effective distance,
optimal paths, visual connectivity and micro-terrain analysis.
Figure 1. Spatial Analysis and
Spatial Statistics are extensions of traditional ways of analyzing mapped data.
In
addition, it provides a mathematical/statistical framework by numerically
representing geographic space. Traditional
Statistics is inherently non-spatial as it seeks to represent a data
set by its typical response regardless of spatial patterns. The mean, standard deviation and other
statistics are computed to describe the central tendency of the data in
abstract numerical space without regard to the relative positioning of the data
in real-world geographic space.
Spatial
Statistics, on the other hand, extends traditional statistics
on two fronts. First, it seeks to map
the variation in a data set to show where unusual responses occur, instead of
focusing on a single typical response.
Secondly, it can uncover “numerical spatial relationships” within and
among mapped data layers, such as generating a prediction map identifying where
likely customers are within a city based on existing sales and demographic
information.
The
next few sections investigate important aspects and procedures in Spatial
Analysis and Spatial Statistics through a couple of example applications in
natural resources and geo-business.
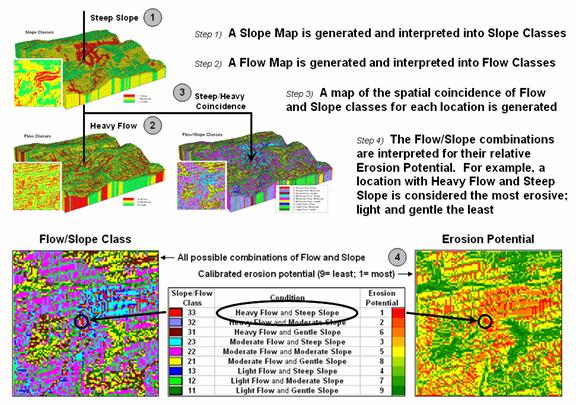
Figure 2 shows the processing logic for generating a map of potential
erosion for part of a large watershed.
The model assumes that erosion potential is primarily a function of
terrain steepness and water flow.
Admittedly the model is simplistic but serves as a good starting point
for a spatial analysis example in natural resources.
Figure 2. Erosion potential is in
large part dependent on the spatial combination of slope and flow.
The
first step calculates a slope map that is interpreted into three classes of relative
steepness—gentle (green), moderate (yellow) and steep (red) terrain. Similarly, an accumulation flow map is
generated and then interpreted into three classes of surface confluence—light
(green), moderate (yellow) and heavy (red) overland flows. The slope and flow maps are shown draped over
the terrain surface to help visually verify the results. How the slope and flow maps were derived has
been discussed in previous columns focusing on procedures and algorithms
involved. What is important for this
discussion is the realization that realistic spatial considerations beyond our
paper-map legacy can be derived and incorporated into map processing logic.
The
third step combines the two maps into nine possible coincidence combinations
and then interprets the combinations into relative erosion potential. For example, areas with heavy flows and steep
slopes have the greatest potential for erosion while areas that have light
flows and gentle slopes have the least.
At this point, the calibration identifying relative erosion potential
should raise some concern, but discussion of this critical step is reserved for
later. What is important at this point
is a basic understanding of the spatial reasoning supporting the model’s
logic.
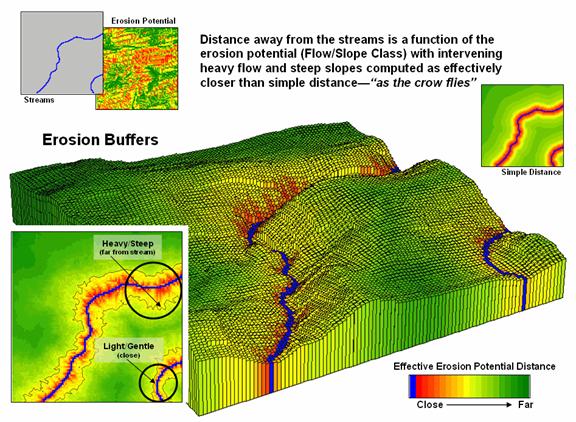
The
Erosion Potential map in figure 2 clearly shows that not all locations have the
same potential to get dirt balls rolling downhill. Given this information, a series of simple
buffers based on planimetric distance would be ludicrous for protecting against
sediment loading to streams. It is
common sense that a fixed distance likely would be an insufficient setback in
areas of high erosion potential with heavy flows and steep intervening
conditions. Similarly the buffer would
reach too far in conditions of light flow and gentle slopes.
Figure 3. Effective distance from
streams considering erosion potential generate realistic protective buffers.
Figure
3 shows an extension of the model that reaches farther from streams under
adverse erosion conditions and not as far in favorable conditions. The result is a buffer that constricts and
expands with erosion potential around the streams. While this “rubber-ruler” approach to
establishing protective buffers isn’t part of our traditional map paradigm, it
is part of real-world experience that recognizes “all buffer-feet are not the
same.”
This
simple example of a Spatial Analysis application illustrates how the evolution
of
Bending
Our Understanding of Distance
(GeoWorld, January 2005)
The last
section introduced two dominant forces that are moving mapping toward map
analysis. Spatial Statistics is used to characterize the geographic
distribution in a set of data and uncover the “numerical spatial relationships”
among data layers. Spatial Analysis extends traditional discrete map objects of point,
lines and polygons to continuous surfaces that support a wealth of new
analytical operations for characterizing “contextual spatial relationships.”
In
describing spatial analysis, an example of generating an effective erosion
buffer was used. A comparison of simple
distance (as the crow flies) and effective distance (as the crow walks) showed
how a more realistic protective buffer around a stream expands and contracts
depending on the erosion potential conditions surrounding the stream. What was left unexplained was how the
computer calculates the effective distance short of using a rubber ruler.
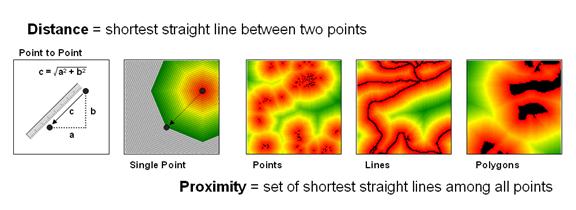
The
left side of figure 1 diagrams how we traditionally measure distance between
two points—manually and mathematically.
We can place a ruler alongside the points and note the number of
tic-marks separating them, and then multiply the map distance times the scale
factor to determine the geographic distance.
Or we can calculate the X and Y differences between the points’
coordinates and use the Pythagorean Theorem to solve for the shortest straight
line distance between two points (hypotenuse of a right triangle).
Spatial
analysis takes the concept of distance a bit farther to that of proximity—the
set of shortest straight lines among all points within a geographic area. It is calculated as a series of distance
waves that move out from one of the points.
In effect this process is analogous to nailing a ruler at the point and
spinning it with the tic-marks scribing concentric circles of distance. The distance to any point within a project
area is simply its stored value indicating the number of rings away from the
starting location.
Figure 1. Distance measures the
space between two points while proximity identifies the spacing throughout a
continuous geographic area.
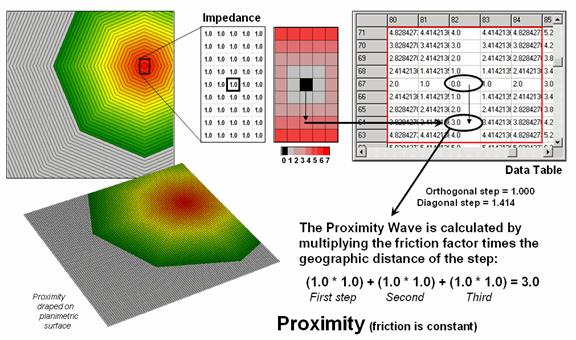
Figure 2. Simple proximity
considers uniform impedance as a Proximity Wave front propagates away from a
starting location—“as the crow flies.”
If more
than one feature is considered (sets of starting points, lines or polygons) the
computer successively calculates proximity a starting location at a time, and
keeps track of the shortest distance that is calculated for each map location. The result is a proximity surface that
identifies the distance to the closest starting point. In figure 1 the three maps on the right
identify proximity surfaces for a set of housing locations (points), the entire
road network (lines) and critical habitat areas (polygons).
Figure
2 illustrates the calculations for a portion of the proximity surface shown in
figure 1. The algorithm first identifies
the adjoining grid cell locations that a starting location could move into
(eight adjacent light grey cells). Then
it determines the geographic distance of the step as orthogonal (up/down or
across = 1.000 grid space) or diagonal (slanting = 1.414) and multiples this
distance times its relative impedance factor.
In the case of simple proximity the factor is constant (1.0) throughout
the project area and the result is reduced to simply the geographic distance of
the step.
The
process is repeated for all cells within successive distance rings with the
computer keeping track of the smallest distance value for each location as the
waves advance (like tossing a rock into a pond). Note that the values stored in the table
increment by one in the orthogonal directions (1.0, 2.0, etc) and are adjusted
for longer steps in the diagonal directions (1.414, 2.828, etc.) and
off-diagonal directions (2.414, etc.) as combinations of orthogonal and
diagonal steps.
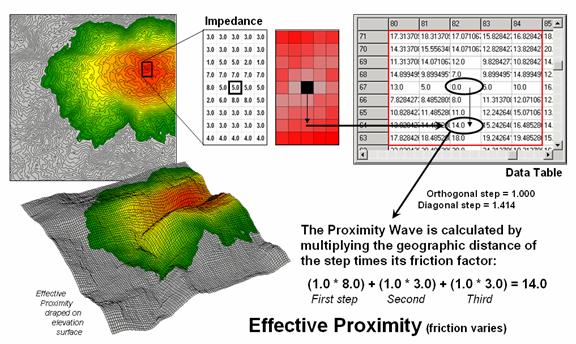
Figure 3. Effective proximity
considers varying impedance that changes with intervening conditions—“as the
crow walks.”
Effective
proximity relaxes the assumption that the relative ease of movement (impedance)
is the same throughout a project area.
In the example shown in figure 3, the Proximity Wave for the first step
is 1.0 (orthogonal step) times its difficulty of 8.0 (impedance factor) results
in an effective distance of 8.0. The
second step has an effective distance of 3.0 (1.0 * 3.0) and combines for a total
movement of 11.0 (8.0 + 3.0) from the starting location. Note that the movement in the opposite
direction is effectively a little further away ((1.0 * 7.0) + (1.0 * 5.0) =
12.0)). In practice, half steps are used
for more precise calculations (see author’s notes).
In the practical
example discussed in the previous section, a map of erosion potential was used
to identify variable impedance based on slope and flow characteristics of the
surrounding terrain. Areas with high
erosion potential were assigned low friction values and therefore the effective
buffers reached farther than in areas of minimal erosion potential having
higher friction values. The result was a
map of effective protection buffers around streams that expanded and contracted
in response to localized conditions.
Effective
buffers are but one example of a multitude of new spatial analysis procedures
that are altering our traditional view mapped data analysis. The next section will investigate some of the
new procedures in spatial statistics that uncover numerical relationships
within and among map layers.
________________________
Author’s Note: The more
exacting half-step calculation for the example is (0.5 * 5.0) + (0.5 * 8.0) +
(0.5 * 8.0) + (0.5 * 3.0) + (.5 * 3.0) + (.5 * 3.0) = 15.0
Use Spatial Statistics to Map Abnormal Averages
(GeoWorld, February 2005)
The
previous couple of sections identified two dominant forces that are moving mapping
toward map analysis—Spatial Analysis and Spatial Statistics. The discussion focused on Spatial Analysis that supports a wealth
of new analytical operations for characterizing “contextual spatial
relationships.” Now we can turn our
attention to Spatial Statistics and
how it characterizes the geographic distribution of mapped data to uncover the
“numerical spatial relationships.”
Most of
us are familiar with the old “bell-curve” for school grades. You know, with lots of C’s, fewer B’s and
D’s, and a truly select set of A’s and F’s.
Its shape is a perfect bell, symmetrical about the center with the tails
smoothly falling off toward less frequent conditions.
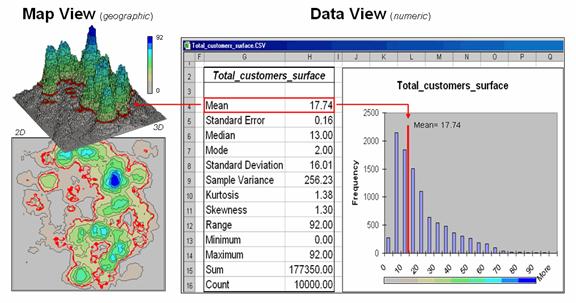
Figure 1. Mapped data are characterized
by their geographic distribution (maps on the left) and their numeric
distribution (descriptive statistics and histogram on the right).
However
the normal
distribution (bell-shaped) isn’t as normal (typical) as you might think
...in the classroom or in
The
geographic distribution of the data is characterized in the map
view by the 2D contour map and 3D surface on the left. Note the distinct geographic pattern of the
surface with bigger bumps (higher customer density) in the central portion of
the project area. As is normally the
case with mapped data, the map values are neither uniformly nor randomly
distributed in geographic space. The
unique pattern is the result of complex spatial processes determining where
people live that are driven by a host of factors—not spurious, arbitrary,
constant or even “normal” events.
Now
turn your attention to the numeric distribution of the data depicted in the
right side of the figure. The data
view was generated by simply transferring the grid values defining the
map surface to Excel, and then applying the Histogram
and Descriptive Statistics options
of the Data Analysis add-in tools. The
mechanics used to plot the histogram and generate the statistics were a
piece-of-cake, but the intellectual challenge is to make some sense of it
all.
Note
that the data aren’t distributed as a normal bell-curve, but appear shifted to
the left. The tallest spike and the
intervals to its left, match the large expanse of grey values in the map view—frequently
occurring values. If the surface
contained disproportionably higher value locations, there would be a spike at
the high end of the histogram. The red
line in the histogram locates the mean (average) value for the numeric
distribution. The red line in the 2D and
3D maps shows the same thing, except it’s identified in the geographic
distribution.
The mental exercise linking geographic space with data space is fundamental to
spatial statistics and leads to important points about the nature of mapped
data. First, there isn’t a fixed
relationship between the two views of the data’s distributions (geographic and
data). For example, a myriad of
geographic patterns can result in the same histogram. That’s because spatial data contains
additional information—where, as well
as what—and the same data summary of
the “what’s” can be reflected in a multitude of spatial arrangements
(“where’s).
But is the reverse true? Can a given
geographic arrangement result in different data views? Nope, and it’s this relationship that
catapults mapping and geo-query into the arena of mapped data analysis. Traditional analysis techniques assume a
functional form for the frequency distribution (histogram shape), with the standard
normal (bell-shaped) being the most prevalent.
Figure
2 offers yet another perspective of the link between numeric and geographic
distributions. The upper-left inset
identifies the spatial pattern formed by 16 samples of the “percent of home equity
loan limit” for a small project area— ranging from 16.8 to 72.4. The table reports the numerical pattern of
the data— mean= 42.88 and standard deviation= 19.57. The coefficient of variation is 45.6%
[(19.57/42.88) * 100= 45.6%] suggesting a fairly large unexplained variation
among the data values.
In a
geographic context, the mean represents a horizontal plane hovering over the
project area. However, the point map
suggests a geographic trend in the data from values lower than the mean in the
west toward higher values in the east.
The inset in the upper-right portion of figure 2 shows a “nearest
neighbor” surface generated by assigning the closest sample value to all of the
other non-sampled grid locations in the project area. While the distribution is blocky it serves as
a first-order estimate of the geographic distribution you see in the point
map—lower in the east and higher in the west.
The
series of plots in the lower portion of figure 2 shows the results of iteratively smoothing the blocky
data. This process repeatedly passes a
“roving window” over the area that calculates the average value within
quarter-mile. The process is analogous
to chipping away at the stair steps with the rubble filling in the bottom. The first smoothing still retains most of the
sharp peak and much of the angular pattern in the blocky surface. As the smoothing progresses the surface takes
on the general geographic trend of the data (Smooth10).
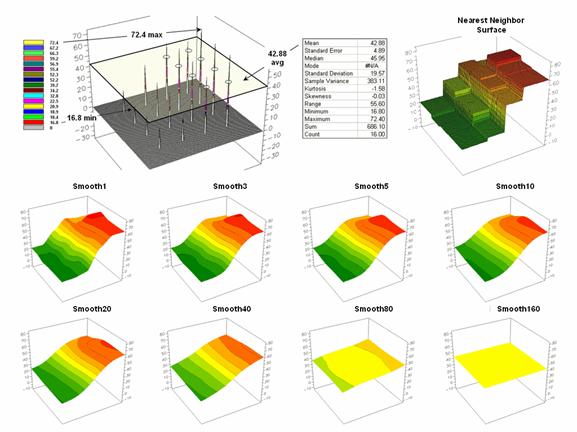
Figure
2. The spatial distribution implied by a
set of discrete sample points can be estimated by iterative smoothing of the
point values.
Eventually
the surface is eroded to a flat plane— the arithmetic mean of the data. The progressive series of plots illustrate a
very important concept in surface modeling— the
geographic distribution maps the variance.
Or, in other words, a map surface uses the geographic pattern in a data
set to help explain the variation among the sample points.
Keep
this in mind the next time you reduce a bunch of sample data to their
arithmetic average and then assign that value to an entire polygon, such as a
sales district, county or other administrative boundary. In essence, this simple mapping procedure
often strips out the inherent spatial information in a set of data—sort of like
throwing the baby out with the bath water.
Making Space for Mapped Data
(GeoWorld, March 2005)
The
past three sections have investigated two dominant forces that are driving
traditional
The
other force, Spatial Statistics, is
used to derive “numerical spatial relationships” that map the variation in a
set of data (surface modeling) and investigate the similarity among map layers
to classify data patterns and develop predictive models (spatial data
mining). This final installment in the
series focuses on the underlying concepts supporting data mining capabilities
of analytical
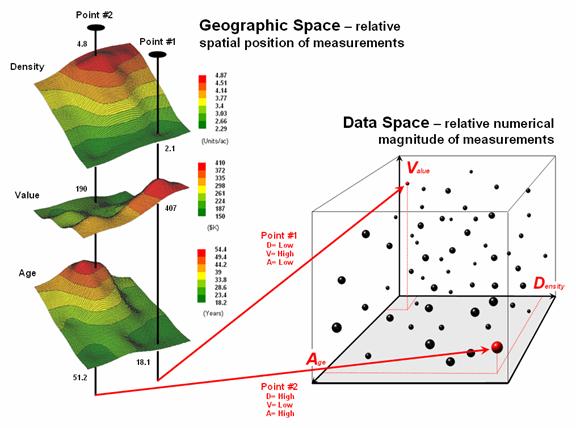
Figure
1. Conceptually linking geographic space
and data space.
The
most fundamental notion is that geographic space and data space are
interconnected. The three maps on the left
side of figure 1 depict surfaces of housing Density, Value and Age for a
portion of a city. It is important that
“maps are numbers first, pictures later” and that the peaks and valleys on the
surfaces are simply the graphic portrayal of actual differences in the values
stored at each map location (grid cell).
The
“data spear” at Point #1 identifies the housing Density as 2.1 units/ac, Value
as $407,000 and Age as 18.3 years and is analogous to your eye noting a color
pattern of green, red, and green. The
other speared location locates a very dissimilar data pattern with
Density= 4.8 units/ac, Value= $190,000
and Age= 51.2 years—or as your eye sees it, a color pattern of red, green and
red.
The
right side of figure 1 depicts how the computer “sees” the data patterns for
the two locations in three-dimensional data space. The three axes defining the extent of the box
correspond to housing Density (D), Value (V) and Age (A). The floating balls represent data patterns of
the grid cells defining the geographic space—one “floating ball” (data point)
for each grid cell. The data values
locating the balls extend from the data axes—2.41, 407.0 and 18.3 for Point
#1. The other point has considerably
higher values in D and A with a much lower V values (4.83, 51.2 and 190.0
respectively) so it plots at a very different location in data space.
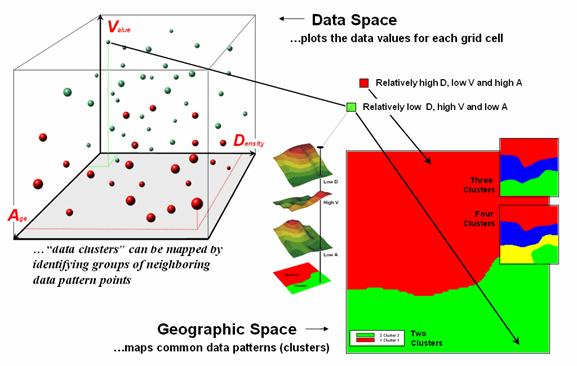
The
fact that similar data patterns plot close to one another in data space with
increasing distance indicating less similarity provides a foothold for mapping
numerical relationships. For example, a
cluster map divides the data into groups of similar data patterns as
schematically depicted in figure 2.
As
noted before the floating balls identify the data patterns for each map
location (geographic space) plotted against the P, K and N axes (data
space). For example, the tiny green ball
in the upper-left corner depicts a map location in the fairly wealthy part of
town (low D, high V and low A). The
large red ball appearing closest to you depicts a location in the less affluent
part (high D, low V and high A).
It
seems sensible that these two extreme responses would belong to different data
groupings (clusters 1 and 2) with the red area locating less wealthy locations
while the green area identifies generally wealthier sections. In a similar fashion, the project area can be
sub-divided into three and four clusters identifying more detailed data pattern
groupings.
While
the specific algorithm used in clustering is beyond the scope of this
discussion, it suffices to note that data distances between the floating balls
are used to identify cluster membership—groups of balls that are relatively far
from other groups and relatively close to each other form separate data
clusters. Other techniques, such as map
similarity and regression, use the link between geographic and data space to
characterize spatial relationships and develop prediction maps.
Figure
2. Data patterns for map locations are
depicted as floating balls in data space that can be grouped into clusters of
similar patterns based on their data distances.
The
realization that mapped data can be expressed in both geographic space and data
space is paramount to a basic understanding of how a computer analyses
numerical interrelationships among mapped data.
Geographic space uses coordinates, such as latitude and
longitude, to locate things in the real world.
The geographic expression of the complete set of measurements depicts
their spatial distribution in familiar map form.
Data
space,
on the other hand, is a bit less familiar.
While you can’t stroll through data space you can conceptualize it and
write algorithms that analyze it … as well as imagine plenty of potential of
applications from geo-business to natural resources. Coupling the power of Spatial Statistics with
that of Spatial Analysis takes traditional statistics and
_____________________
Further Online
Reading: (Chronological
listing posted at www.innovativegis.com/basis/BeyondMappingSeries/)
GIS Represents Spatial Patterns and
Relationships — discusses the important differences
among discrete mapping , continuous map surfaces and map analysis (April 1999)
(Back
to the Table of Contents)