Part 2 – Understanding the Effective Distance Algorithm

Note: These topics appeared in GIS World, Vol.5, No.8 through Vol. 5, No. 10, October December 1992. Also they serve as the basis for portions of Topic 9, Sections 28-30 in Beyond Mapping: Concepts, Algorithms, and Issues in GIS (Berry, 1993; Wiley)

DISTANCE IS SIMPLE AND STRAIGHT FORWARD

For those with a GIS World archive, an overview of the evolving concept of distance was made in the September 1989 issue (GIS World, Vol. 2, No. 5). The objective of this revisiting of the subject focuses on the real stuff-- how a GIS derives a distance map. The basic concept of distance measurement involves two things-- a unit and a procedure. The tic-marks on your ruler establishes the unit. If you are an old wood-cutter like me, a quarter of an inch is good enough. If more accuracy is required, you choose a ruler with finer spacing. The fact that these units are etched on side of a straight-edge implies that the procedure of measurement is "shortest, straight line between two points." You align the ruler between two points and count the tic-marks. There, that's it-- simple, satisfying and comfortable.

But what is a ruler? Actually, it is just one row of an implied grid you have placed over the map. In essence, the ruler forms a reference grid, with the distance between each tic-mark forming one side of a grid cell. You simply align the imaginary grid and count the cells along the row. That's easy for you, but tough for a computer. To measure distance like this, the computer would have to recalculate a transformed reference grid for each measurement. Pythagoras anticipated this potential for computer-abuse several years ago and developed the Pythagorean Theorem. The procedure keeps the reference grid constant and relates the distance between two points as the hypotenuse of a right triangle formed by the grid's rows and columns. There that's it-- simple, satisfying and comfortable for the high school mathematician lurking in all of us.

A GIS that's beyond mapping, however, "asks not what math can do for it, but what it can do for math." How about a different way of measuring distance? Instead of measuring between just two points, let's expand the concept of distance to that of proximity-- distance among sets of points. For a raster procedure, consider the analysis grid on the left side of the accompanying figure. The distance from the cell in the lower-right corner (Col 6, Row 6) to each of its three neighbors is either 1.000 grid space (orthogonal), or 1.414 (diagonal). Similar to the tic-marks on your ruler, the analysis grid spacing can be very small for the exacting types, or fairly course for the rest of us.

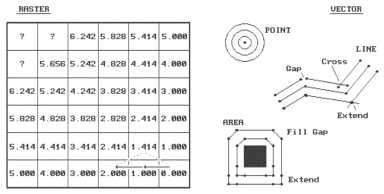
Characterizing Simple Proximity.

The distance to a cell in the next "ring" is a combination of the information in the previous ring and the type of movement to the cell. For example, position Col 4, Row 6 is 1.000 + 1.000= 2.000 grid spaces as the shortest path is orthogonal-orthogonal. You could move diagonal-diagonal passing through position Col 5, Row 5, as shown with the dotted line. But that route wouldn't be "shortest" as it results in a total distance of 1.414 + 1.414= 2.828 grid spaces. The rest of the ring assignments involves a similar test of all possible movements to each cell, retaining the smallest total distance. With tireless devotion, your computer repeats this process for each successive ring. The missing information in the figure allows you to be the hero and complete the simple proximity map. Keep in mind that there are three possible movements from ring cells into each of the adjacent cells. (Hint-- one of the answers is 7.070).

This procedure is radically different from either your ruler or Pythagoras's theorem. It is more like nailing your ruler and spinning it while the tic-marks trace concentric circles-- one unit away, two units away, etc. Another analogy is tossing a rock into a still pond with the ripples indicating increasing distance. One of the major advantages of this procedure is that entire sets of "starting locations" can be considered at the same time. It's like tossing a handful of rocks into the pond. Each rock begins a series of ripples. When the ripples from two rocks meet, they dissipate and indicate the halfway point. The repeated test for the smallest accumulated distance insures that the halfway "bump" is identified. The result is a distance assignment (rippling ring value) from every location to its nearest starting location.

If your conceptual rocks represented the locations of houses, the result would be a map of the distance to the nearest house for an entire study area. Now imagine tossing an old twisted branch into the water. The ripples will form concentric rings in the shape of the branch. If your branch's shape represented a road network, the result would be a map of the distance to the nearest road. By changing your concept of distance and measurement procedure, proximity maps can be generated in an instant compared to the time you or Pythagoras would take.

However, the rippling results are not as accurate for a given unit spacing. The orthogonal and diagonal distances are right on, but the other measurements tend to overstate the true distance. For example, the rippling distance estimate for position 3,1 is 6.242 grid spaces. Pythagoras would calculate the distance as C= ((3**2 + 5**2)) **1/2)= 5.831. That's a difference of .411 grid spaces, or 7% error. As most raster systems store integer values, the rounding usually absorbs the error. But if accuracy between two points is a must, you had better forego the advantages of proximity measurement.

A vector system, with its extremely fine reference grid, generates exact Pythagorean distances. However, proximity calculations are not its forte. The right side of the accompanying figure shows the basic considerations in generating proximity "buffers" in a vector system. First, the "reach" of the buffer is established by the user-- as before, it can be very small for the exacting types, or fairly course for the rest of us. For point features, this distance serves as the increment for increasing radii of a series of concentric circles. Your high school geometry experience with a compass should provide a good conceptualization of this process. The GIS, however, evaluates the equation for a circle given the center and radius to solve for the end points of the series of line segments forming the boundary.

For line and area features, the reach is used to increment a series of parallel lines about the feature. Again, your compass work in geometry should rekindle the draftsman's approach. The GIS, on the other hand, uses the slope of each line segment and the equation for a straight line to calculate the end points of the parallel lines. "Crosses" and "gaps" occur wherever there is a bend. The intersection of the parallel lines on inside bends are clipped and the intersection is used as the common end point. Gaps on outside bends present a different problem. Some systems simply fill the gaps with a new line segment. Others extend the parallel lines until they intersect. The buffers around the square feature shows that these two approaches can have radically different results. You can even take an additional step and fit a spline-fitting algorithm to smooth the lines.

A more important concern is how to account for "buffer bumping." It's only moderately taxing to calculate the series buffers around individual features, but it's a monumental task to identify and eliminate any buffer overlap. Even the most elegant procedure requires a ponderous pile of computer code and prodigious patience by the user. Also, the different approaches produce different results, affecting data exchange and integration among various systems. The only guarantee is that a stream proximity map on system A will be different than a stream proximity map on system B.

Another guarantee is that new concepts of distance are emerging as GIS goes beyond mapping. Next issue will focus on the twisted concept of "effective" proximity which is anything but simple and straight forward.

_____________________

As with all Beyond Mapping articles, allow me to apologize in advance for the "poetic license" invoked in this terse treatment of a complex subject. Readers interested in more information on distance algorithms should consult the classic text, The Geography of Movement, by Lowe and Moryadas, 1975, Houghton Miffen publishers.

RUBBER RULERS...

It must be a joke, like a left-handed wrench, a bucket of steam or a snipe hunt. Or it could be the softening of blows in the classroom through enlightened child-abuse laws. Actually, a rubber ruler often is more useful and accurate than the old straight-edge version. It can bend, compress and stretch throughout a mapped area as different features are encountered. After all it's more realistic, as the straight path is rarely what most of us follow.

Last issue established the procedure for computing simple proximity maps as forming a series of concentric rings. The ability to characterize the continuous distribution of simple, straight-line distances to sets of features like houses and roads is useful in a multitude of applications. More importantly, the GIS procedure allows measurement of effective proximity recognizing absolute and relative barriers to movement, as shown in the accompanying figure. As discussed in the last issue, the proximity to the starting location at Col 6, Row 6 is calculated as a series of rings. However, this time we'll use the map on the left containing "friction" values to incorporate the relative ease of movement through each grid cell. A friction value of 2.00 is twice as difficult to cross as one with 1.00. Absolute barriers, such as a lake to a non-swimming hiker, are identified as infinitely far away and forces all movement around these areas.

Step DistanceN= .5 * (GSdistance * FfactorN)

Accumulated Distance= Previous + Sdistance1 + Sdistance2

Minimum Adistance is Shortest, Non-Straight Distance

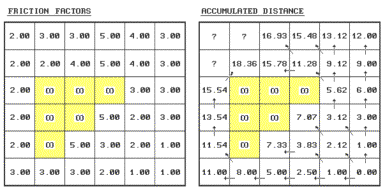
Characterizing Effective Proximity.

A generalized procedure for calculating effective distance using the friction values is as follows (refer to the figure).

Step 1 - identify the ring cells ("starting cell" 6,6 for first iteration).

Step 2 - identify the set of immediate adjacent cells (positions 5,5; 5,6; and 6,5 for first iteration).

Step 3 - note the friction factors for the ring cell and the set of adjacent cells (6,6=1.00; 5,5=2.00; 5,6=1.00; 6,5=1.00).

Step 4 - calculate the distance, in half-steps, to each of the adjacent cells from each ring cell by multiplying 1.000 for orthogonal or 1.414 for diagonal movement by the corresponding friction factor...

.5 * (GSdirection * Friction Factor)

For example, the first iteration ring from the center of 6,6 to the center of position

5,5 is .5 * (1.414 * 1.00)= .707

.5 * (1.414 * 2.00)= 1.414

2.121

5,6 is .5 * (1.000 * 1.00)= .500

.5 * (1.000 * 1.00)= .500

1.000

6,5 is .5 * (1.000 * 1.00)= .500

.5 * (1.000 * 1.00)= .500

1.000

Step 5 - choose the smallest accumulated distance value for each of the adjacent cells.

Repeat - for successive rings, the old adjacent cells become the new ring cells (the next iteration uses 5,5; 5,6 and 6,5 as the new ring cells).

Whew! That's a lot of work. Good thing you have a silicon slave to do the dirty work. Just for fun (ha!) let's try evaluating the effective distance for position 2,1...

If you move from position 3,1 its

.5 * (1.000 * 3.00)= 1.50

.5 * (1.000 * 3.00)= 1.50

3.00

plus previous distance= 16.93

equals accumulated distance= 19.93

If you move from position 3,2 its

.5 * (1.414 * 4.00)= 2.83

.5 * (1.414 * 3.00)= 2.12

4.95

plus previous distance= 15.78

equals accumulated distance= 20.73

If you move from position 2,2 its

.5 * (1.000 * 2.00)= 1.00

.5 * (1.000 * 3.00)= 1.50

2.50

plus previous distance= 18.36

equals accumulated distance= 20.86

Finally, choose the smallest accumulated distance value of 19.93, assign it to position 2,1 and draw a horizontal arrow from position 3,1. Provided your patience holds, repeat the process for the last two positions (answers in the next issue).

The result is a map indicating the effective distance from the starting location(s) to everywhere in the study area. If the "friction factors" indicate time in minutes to cross each cell, then the accumulated time to move to position 2,1 by the shortest route is 19.93 minutes. If the friction factors indicate cost of haul road construction in thousands of dollars, then the total cost to construct a road to position 2,1 by the least cost route is $19,930. A similar interpretation holds for the proximity values in every other cell.

To make the distance measurement procedure even more realistic, the nature of the "mover" must be considered. The classic example is when two cars start moving toward each other. If they travel at different speeds, the geographic midpoint along the route will not be the location the cars actually meet. This disparity can be accommodated by assigning a "weighting factor" to each starter cell indicating its relative movement nature-- a value of 2.00 indicates a mover that is twice as "slow" as a 1.00 value. To account for this additional information, the basic calculation in Step 4 is expanded to become

.5 * (GSdirection * Friction Factor * Weighting Factor)

Under the same movement direction and friction conditions, a "slow" mover will take longer to traverse a given cell. Or, if the friction is in dollars, an "expensive" mover will cost more to traverse a given cell (e.g., paved versus gravel road construction).

I bet your probing intellect has already taken the next step-- dynamic effective distance. We all know that real movement involves a complex interaction of direction, accumulation and momentum. For example, a hiker walks slower up a steep slope than down it. And, as the hike gets longer and longer, all but the toughest slow down. If a long, steep slope is encountered after hiking several hours, most of us interpret it as an omen to stop for quiet contemplation.

The extension of the basic procedure to dynamic effective distance is still in the hands of GIS researchers. Most of the approaches use a "look-up table" to update the "friction factor" in Step 4. For example, under ideal circumstances you might hike three miles an hour in gentle terrain. When a "ring" encounters an adjacent cell which is steep (indicated on the slope map) and the movement is uphill (indicated on the aspect map), the normal friction is multiplied by the "friction multiplier" in the look-up table for the "steep-up" condition. This might reduce your pace to one mile per hour. A three-dimensional table can be used to simultaneously introduce fatigue-- the "steep-up-long" condition might equate to zero miles per hour.

See how far you have come? From the straight forward interpretation of distance ingrained in your ruler and Pythagoras's theorem, to the twisted movement around and through intervening barriers. This bazaar discussion should confirm that GIS is more different than it is the same as traditional mapping. The next issue will discuss how the shortest, but "not necessarily straight path," is identified.

_____________________

As with all Beyond Mapping articles, allow me to apologize in advance for the "poetic license" invoked in this terse treatment of a complex subject. Readers with the pMAP Tutorial disk should review the slide show and tutorial on "Effective Sediment Loading." An excellent discussion of effective proximity is in C. Dana Tomlin's text, Geographical Information Systems and Cartographic Modeling, available through the GIS World Bookshelf.

COMPUTING CONNECTIVITY

...all the right connections.

The last couple of articles challenged the assumption that all distance measurement is the "shortest, straight line between two points." The concept of proximity relaxed the "between two points" requirement. The concept of movement, through absolute and relative barriers, relaxed the "straight line" requirement. What's left? --"shortest," but not necessarily straight and often among sets points.

Where does all this twisted and contorted logic lead? That's the point-- connectivity. You know, "the state of being connected," as Webster would say. Since the rubber ruler algorithm relaxed the simplifying assumption that all connections are straight, it seems fair to ask, "then what is the shortest route, if it isn't straight." In terms of movement, connectivity among features involves the computation of optimal paths. It all starts with the calculation of an "accumulation surface," like the one shown on the left side of the accompanying figure. This is a three-dimensional plot of the accumulated distance table you completed last month. Remember? Your homework involved that nasty, iterative, five-step algorithm for determining the friction factor weighted distances of successive rings about a starting location. Whew! The values floating above the surface are the answers to the missing table elements-- 17.54, 19.54 and 19.94. How did you do?

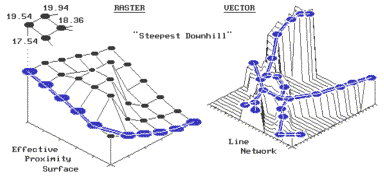Establishing Shortest, Non-Straight Routes.

But that's all behind us. By comparison, the optimal path algorithm is a piece of cake-- just choose the steepest downhill path over the accumulated surface. All of the information about optimal routes is incorporated in the surface. Recall, that as the successive rings emanate from a starting location, they move like waves bending around absolute barriers and shortening in areas of higher friction. The result is a "continuously increasing" surface which captures the shortest distance as values assigned to each cell.

In the "raster" example shown in the figure, the steepest downhill path from the upper left corner (position 1,1) moves along the left side of the "mountain" of friction in the center. The path is determined by successively evaluating the accumulated distance of adjoining cells and choosing the smallest value. For example, the first step could move to the right (to position 2,1) from 19.54 to 19.94 units away. But that would be stupid, as it is farther away than the starting position itself. The other two potential steps, to 18.36 or 17.54, make sense, but 17.54 makes the most sense as it gets you a lot closer. So you jump to the lowest value at position 1,2. The process is repeated until you reach the lowest value of 0.0 at position 6,6.

Say, that's where we started measuring distance. Let's get this right-- first you measure distance from a location (effective distance map), then you identify another location and move downhill like a rain drop on a roof. Yep, that's it. The path you trace identifies the route of the distance wave-front (successive rings) that got there first-- shortest. But why stop there, when you could calculate optimal path density? Imagine commanding your silicon slave to compute the optimal paths from all locations down the surface, while keeping track of the number of paths passing through each location. Like gullies on a terrain surface, areas of minimal impedance collect a lot of paths. Ready for another step?-- weighted optimal path density. In this instance, you assign an importance value (weight) to each starting location, and, instead of merely counting the number of paths through each location, you sum the weights.

For the techy types, the optimal path algorithm for raster systems should be apparent. It's just a couple of nested loops that allow you to test for the biggest downward step of "accumulated distance" among the eight neighboring cells. You move to that position and repeat. If two or more equally optimal steps should occur, simply move to them. The algorithm stops when there aren't any more downhill steps. The result is a series of cells which form the optimal path from the specified "starter" location to the bottom of the accumulation surface. Optimal path density requires you to build another map that counts the number paths passing through each cell. Weighted optimal path density sums the weights of the starter locations, rather than simply counting them.

The vector solution is similar in concept, but its algorithm is a bit more tricky to implement. In the above discussion, you could substitute the words "line segment" for "cell" and not be too far off. First, you locate a starting location on a network of lines. The location might be a fire station on a particular street in your town. Then you calculate an "accumulation network" in which each line segment end point receives a value indicating shortest distance to the fire station along the street network. To conceptualize this process, the raster explanation used rippling waves from a tossed rock in a pond. This time, imagine waves rippling along a canal system. They are constrained to the linear network, with each point being farther away than the one preceding it. The right side of the accompanying figure shows a three-dimensional plot of this effect. It looks a lot like a roll-a-coaster track with the bottom at the fire station (the point closest to you). Now locate a line segment with a "house-on-fire." The algorithm hops from the house to "lily pad to lily pad" (line segment end points), always choosing the smallest value. As before, this "steepest downhill" path traces the wave-front that got there first-- shortest route to the fire. In a similar fashion, the concepts of optimal path density and weighted optimal path density from multiple starting locations remain intact.

What makes the vector solution testier is that the adjacency relationship among the lines is not as neatly organized as in the raster solution. This relationship, or "topology," describing which cell abuts which cell is implicit in the matrix of numbers. On the other hand, the topology in a vector system must be stored in a database. A distinction between a vertex (point along a line) and a node (point of intersecting lines) must be maintained. These points combine to form chains which, in a cascading fashion, relate to one another. Ingenuity in database design and creative use of indices and pointers for quick access to the topology are what separates one system from another. Unfettered respect should be heaped upon the programming wizards that make all this happen.

However, regardless of the programming complexity, the essence of the optimal path algorithm remains the same-- measure distance from a location (effective distance map), then locate another location and move downhill. Impedance to movement can be absolute and relative barriers such as one-way streets, no left turn and speed limits. These "friction factors" are assigned to the individual line segments, and used to construct an accumulation distance network in a manner similar to that discussed last month. It is just that in a vector system, movement is constrained to an organized set of lines, instead of an organized set of cells.

Optimal path connectivity isn't the only type of connection between map locations. Consider narrowness-- the shortest cord connecting opposing edges. Like optimal paths, narrowness is a two part algorithm based on accumulated distance. For example, to compute a narrowness map of a meadow your algorithm first selects a "starter" location within the meadow. It then calculates the accumulated distance from the starter until the successive rings have assigned a value to each of the meadow edge cells. Now choose one of the edge cells and determine the "opposing" edge cell which lies on a straight line through the starter cell. Sum the two edge cell distance values to compute the length of the cord. Iteratively evaluate all of the cords passing through the starter cell, keeping track of the smallest length. Finally, assign the minimum length to the starter cell as its narrowness value. Move to another meadow cell and repeat the process until all meadow locations have narrowness values assigned.

As you can well imagine, this is a computer-abusive operation. Even with algorithm trickery and user limits, it will send the best of workstations to "deep space" for quite awhile. Particularly when the user wants to compute the "effective narrowness" (non-straight cords respecting absolute and relative barriers) of all the timber stands within a 1000x1000 map matrix. But GIS isn't just concerned with making things easy; be it for man or machine. It is for making things more realistic which, hopefully, leads to better decisions. Optimal path and narrowness connectivity are uneasy concepts leading in that direction.