Excerpts on Diversity and Interspersion/Juxtaposition Indices from...
FRAGSTATS: Spatial Pattern Analysis Program for
Quantifying Landscape Structure
An Updated Version of the USDA Forest Service - General Technical Report PNW-GTR-351 (August 1995). A complete version of this comprehensive publication on Landscape Structure Analysis is available online at www.innovativegis.com, select FRAGSTATS*ARC, FRAGSTATS Manual. For more information on FRAGSTATS indices, contact Dr. McGarigal at McGarigalK@forwild.umass.edu.
________________________________________________________
(Excerpt from Chapter 4: FRAGSTATS Metrics Overview) Diversity Metrics FRAGSTATS computes several statistics that quantify diversity at the landscape level (Table 1). These metrics quantify landscape composition. Diversity measures have been used extensively in a variety of ecological applications. They originally gained popularity as measures of plant and animal species diversity. There has been a proliferation of diversity indices and we will make no attempt to review them here. FRAGSTATS computes 3 diversity indices. These diversity measures are influenced by 2 components--richness and evenness. Richness refers to the number of patch types present; evenness refers to the distribution of area among different types. Richness and evenness are generally referred to as the compositional and structural components of diversity, respectively. Some indices (e.g., Shannon's diversity index) are more sensitive to richness than evenness. Thus, rare types have a disproportionately large influence on the magnitude of the index. Other indices (e.g., Simpson's diversity index) are relatively less sensitive to richness and thus place more weight on the common species. These diversity indices have been applied by landscape ecologists to measure 1 aspect of landscape structure--landscape composition (e.g., Romme 1982, O'Neill et al. 1988, Turner 1990a).The most popular diversity index is Shannon's diversity index (SHDI) based on information theory (Shannon and Weaver 1949). The value of this index represents the amount of "information" per individual (or patch, in this case). Information is a somewhat abstract mathematical concept that we will not attempt to define. The absolute magnitude of Shannon's diversity index is not particularly meaningful; therefore, it is used as a relative index for comparing different landscapes or the same landscape at different times. Simpson's diversity index (SIDI) is another popular diversity measure that is not based on information theory (Simpson 1949). Simpson's index is less sensitive to the presence of rare types and has an interpretation that is much more intuitive than Shannon's index. Specifically, the value of Simpson's index represents the probability that any types selected at random would be different types. Thus, the higher the value the greater the likelihood that any 2 randomly drawn patches would be different patch types (i.e., greater diversity). Because Simpson's index is a probability, it can be interpreted in both absolute and relative terms. FRAGSTATS also computes a modified Simpson's diversity index (MSIDI) based on Pielou's (1975) modification of Simpson's diversity index; this index was used by Romme (1982). The modification eliminates the intuitive interpretation of Simpson's index as a probability, but transforms the index into one that belongs to a general class of diversity indices to which Shannon's diversity index belongs (Pielou 1975). Thus, the modified Simpson's and Shannon's diversity indices are similar in many respects and have the same applicability.
The use of diversity measures in community ecology has been heavily criticized because diversity conveys no information on the actual species composition of a community. Species diversity is a community summary measure that does not take into account the uniqueness or potential ecological, social, or economical importance of individual species. A community may have high species diversity yet be comprised largely of common or undesirable species. Conversely, a community may have low species diversity yet be comprised of especially unique, rare, or highly desired species. Although these criticisms have not been discussed explicitly with regards to the landscape ecological application of diversity measures, these criticisms are equally valid when diversity measures are applied to patch types instead of species. In addition, these diversity indices combine richness and evenness components into a single measure, even though it is usually more informative to evaluate richness and evenness independently.
Patch richness (PR) measures the number of patch types present; it is not affected by the relative abundance of each patch type or the spatial arrangement of patches. Therefore, 2 landscapes may have very different structure yet have the same richness. For example, 1 landscape may be comprised of 96% patch type A and 1% each of patch types B-E, whereas another landscape may be comprised of 20% each of patch types A-E. Although, patch richness would be the same, the functioning of these landscapes and the structure of the animal and plant communities would likely be greatly different. Because richness does not account for the relative abundance of each patch type, rare patch types and common patch types contribute equally to richness. Nevertheless, patch richness is a key element of landscape structure because the variety of landscape elements present in a landscape can have an important influence on a variety of ecological processes. Because many organisms are associated with a single patch type, patch richness often correlates well with species richness (McGarigal and McComb, unpubl. data).
Richness is partially a function of scale. Larger areas are generally richer because there is generally greater heterogeneity over larger areas than over comparable smaller areas. This contributes to the species-area relationship predicted by island biogeographic theory (MacArthur and Wilson 1967). Therefore, comparing richness among landscapes that vary in size can be problematic. Patch richness density (PRD) standardizes richness to a per area basis that facilitates comparison among landscapes, although it does not correct for this interaction with scale. FRAGSTATS also computes a relative richness index. Relative patch richness (RPR) is similar to patch richness, but it represents richness as a percentage of the maximum potential richness as specified by the user (Romme 1982). This form may have more interpretive value than absolute richness or richness density in some applications. Note that relative patch richness and patch richness are completely redundant and would not be used simultaneously in any subsequent statistical analysis.
Evenness measures the other aspect of landscape composition--the distribution of area among patch types. There are numerous ways to quantify evenness and most diversity indices have a corresponding evenness index derived from them. In addition, evenness can be expressed as its compliment--dominance (i.e., evenness = 1 - dominance). Indeed, dominance has often been the chosen form in landscape ecological investigations (e.g., O'Neill et al. 1988, Turner et al. 1989, Turner 1990a), although we prefer evenness because larger values imply greater landscape diversity. FRAGSTATS computes 3 evenness indices (Shannon's evenness index, SHEI; Simpson's evenness index, SIEI; modified Simpson's evenness index, MSIEI), corresponding to the 3 diversity indices. Each evenness index isolates the evenness component of diversity by controlling for the contribution of richness to the diversity index. Evenness is expressed as the observed level of diversity divided by the maximum possible diversity for a given patch richness. Maximum diversity for any level of richness is based on an equal distribution among patch types. Therefore, the observed diversity divided by the maximum diversity (i.e., equal distribution) for a given number of patch types represents the proportional reduction in the diversity index attributed to lack of perfect evenness. As the evenness index approaches 1, the observed diversity approaches perfect evenness.
Because evenness is represented as a proportion of maximum evenness, Shannon's evenness index does not suffer from the limitation of Shannon's diversity index with respect to interpretability. Nevertheless, it is important to note that evenness, like richness and diversity, does not convey any information about which patch types are most or least abundant or which may be of greater ecological significance.
Contagion and Interspersion Metrics FRAGSTATS computes 2 indices representing patch interspersion and juxtaposition at the class and landscape levels, although 1 index applies only to the landscape level (Table 1). These metrics quantify landscape configuration. A contagion index was proposed first by O'Neill et al. (1988) and subsequently it has been widely used (Turner and Ruscher 1988, Turner 1989, Turner et al. 1989, Turner 1990a and b, Graham et al. 1991, Gustafson and Parker 1992). Li and Reynolds (1993) showed that the original formula was incorrect; they introduced 2 forms of an alternative contagion index that corrects this error and has improved performance. Both contagion indices are designed for raster images in which each cell is individually evaluated for adjacency, and like-adjacencies (cells not on a patch perimeter) are considered. Both indices have been applied at the landscape level to measure landscape structure.FRAGSTATS computes 1 of the contagion indices proposed by Li and Reynolds (1993). This contagion index (CONTAG) is applicable only to raster images at the landscape level and it is based on raster "cell" adjacencies, not "patch" adjacencies. This contagion index consists of the sum, over patch types, of the product of 2 probabilities: (1) the probability that a randomly chosen cell belongs to patch type i (estimated by the proportional abundance of patch type i), and (2) the conditional probability that given a cell is of patch type i, one of its neighboring cells belongs to patch type j (estimated by the proportional abundance of patch type i adjacencies involving patch type j). The product of these probabilities equals the probability that 2 randomly chosen adjacent cells belong to patch type i and j. This contagion index is appealing because of the straightforward and intuitive interpretation of this probability. Contagion measures both patch type interspersion (i.e., the intermixing of units of different patch types) as well as patch dispersion (i.e., the spatial distribution of a patch type). All other things being equal, a landscape in which the patch types are well interspersed will have lower contagion than a landscape in which patch types are poorly interspersed. According to the previous authors, contagion measures the extent to which landscape elements (patch types) are aggregated or clumped (i.e., dispersion); higher values of contagion may result from landscapes with a few large, contiguous patches, whereas lower values generally characterize landscapes with many small and dispersed patches. Thus, holding interspersion constant, a landscape in which the patch types are aggregated into larger, contiguous patches will have greater contagion than a landscape in which the patch types are fragmented into many small patches. Contagion measures dispersion in addition to patch type interspersion because cells, not patches, are evaluated for adjacency. Landscapes consisting of large, contiguous patches have a majority of internal cells with like adjacencies. In this case, contagion is high because the proportion of total cell adjacencies comprised of like adjacencies is very large and the distribution of adjacencies among edge types is very uneven. Moreover, the contagion index represents the observed level of contagion as a percentage of the maximum possible given the total number of patch types.
We present a new interspersion and juxtaposition index (IJI) that is compatible with both vector and raster images and applicable at both the class and landscape levels. Unlike the earlier contagion indices that are based on raster "cell" adjacencies, our index is based on "patch" adjacencies. Each patch is evaluated for adjacency with all other patch types; like adjacencies are not possible because a patch can never be adjacent to a patch of the same type. For raster images, internal cells are ignored; only the patch perimeters are considered in determining the total length of each unique edge type. Because this index is a measure of "patch" adjacency and not "cell" adjacency, the interpretation is somewhat different than the contagion index. The interspersion index measures the extent to which patch types are interspersed (not necessarily dispersed); higher values result from landscapes in which the patch types are well interspersed (i.e., equally adjacent to each other), whereas lower values characterize landscapes in which the patch types are poorly interspersed (i.e., disproportionate distribution of patch type adjacencies). The interspersion index is not directly affected by the number, size, contiguity, or dispersion of patches per se, as is the contagion index. Consequently, a landscape containing 4 large patches, each a different patch type, and a landscape of the same extent containing 100 small patches of 4 patch types will have the same index value if the patch types are equally interspersed (or adjacent to each other based on the proportion of total edge length in each edge type); whereas, the value of contagion would be quite different. Like the contagion index, the interspersion index is a relative index that represents the observed level of interspersion as a percentage of the maximum possible given the total number of patch types.
Unlike the contagion index, the interspersion and juxtaposition index can be applied at both the class and landscape levels. At the class level, this index measures the juxtapositioning of a focal patch type with all others and does not reflect the interspersion of other patch types. Again, the index is not affected by the dispersion of the focal patch type per se, except that a well dispersed patch type is more likely to be well interspersed as well. For example, the focal patch type could be aggregated in 1 portion of the landscape or maximally dispersed and the value of the index would be the same if the proportion of total edge length involving the focal patch and each other patch type is the same.
It is important to note the differences between the contagion index and the interspersion and juxtaposition index. Contagion is affected by both interspersion and dispersion. The interspersion and juxtaposition index, in contrast, is affected only by patch type interspersion and juxtaposition and not necessarily by the size, contiguity, or dispersion of patches. Thus, although often indirectly affected by dispersion, the interspersion and juxtaposition index directly measures patch type interspersion, whereas contagion measures a combination of both patch type interspersion and dispersion. In addition, contagion and interspersion are inversely related to each other. Higher contagion generally corresponds to lower interspersion and vice versa. Finally, in contrast to the interspersion and juxtaposition index, the contagion index is strongly affected by the grain size or resolution of the image. Given a particular patch mosaic, a smaller grain size will result in greater contagion because of the proportional increase in like adjacencies from internal cells. The interspersion and juxtaposition index is not affected because it considers only patch edges. This scale effect should be carefully considered when attempting to compare results from different studies.
(Excerpt from Chapter 5: Definition and Description of FRAGSTATS Metrics, Landscape Metrics)(L36) Shannon's Diversity Index
![]()
Units: None
Range: SHDI
³ 0, without limitSHDI = 0 when the landscape contains only 1 patch (i.e., no diversity). SHDI increases as the number of different patch types (i.e., patch richness, PR) increases and/or the proportional distribution of area among patch types becomes more equitable.
Description: SHDI equals minus the sum, across all patch types, of the proportional abundance of each patch type multiplied by that proportion.
(L37) Simpson's Diversity Index
Units: None
Range: 0
£ SIDI < 1SIDI = 0 when the landscape contains only 1 patch (i.e., no diversity). SIDI approaches 1 as the number of different patch types (i.e., patch richness, PR) increases and the proportional distribution of area among patch types becomes more equitable.
Description: SIDI equals 1 minus the sum, across all patch types, of the proportional abundance of each patch type squared.
(L38) Modified Simpson's Diversity Index
Units: None
Range: MSIDI
³ 0MSIDI = 0 when the landscape contains only 1 patch (i.e., no diversity). MSIDI increases as the number of different patch types (i.e., patch richness, PR) increases and the proportional distribution of area among patch types becomes more equitable.
Description: MSIDI equals minus the logarithm of the sum, across all patch types, of the proportional abundance of each patch type squared.
(L39) Patch Richness
![]()
Units: None
Range: PR
³ 1, without limitDescription: PR equals the number of different patch types present within the landscape boundary.
(L40) Patch Richness Density
Units: Number per 100 hectares
Range: PRD > 0, without limit
Description: PR equals the number of different patch types present within the landscape boundary divided by total landscape area (m2), multiplied by 10,000 and 100 (to convert to 100 hectares).
(L41) Relative Patch Richness
![]()
Units: Percent
Range: 0 < RPR
£ 100RPR approaches 0 when the landscape contains a single patch type, yet the number of potential patch types is very large. RPR = 100 when all possible patch types are represented in the landscape. RPR is reported as "NA" in the "basename".full file and a dot "." in the "basename".land file if the maximum number of classes is not specified by the user.
Description: RPR equals the number of different patch types present within the landscape boundary divided by the maximum potential number of patch types based on the patch type classification scheme, multiplied by 100 (to convert to percent).
(L42) Shannon's Evenness Index
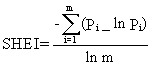 Units:
None
Units:
None
Range: 0
£ SHEI £ 1SHDI = 0 when the landscape contains only 1 patch (i.e., no diversity) and approaches 0 as the distribution of area among the different patch types becomes increasingly uneven (i.e., dominated by 1 type). SHDI = 1 when distribution of area among patch types is perfectly even (i.e., proportional abundances are the same).
Description: SHEI equals minus the sum, across all patch types, of the proportional abundance of each patch type multiplied by that proportion, divided by the logarithm of the number of patch types. In other words, the observed Shannon's Diversity Index divided by the maximum Shannon's Diversity Index for that number of patch types.
(L43) Simpson's Evenness Index
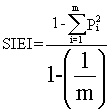
Units: None
Range: 0
£ SIEI £ 1SIDI = 0 when the landscape contains only 1 patch (i.e., no diversity) and approaches 0 as the distribution of area among the different patch types becomes increasingly uneven (i.e., dominated by 1 type). SIDI = 1 when distribution of area among patch types is perfectly even (i.e., proportional abundances are the same).
Description: SIEI equals 1 minus the sum, across all patch types, of the proportional abundance of each patch type squared, divided by 1 minus 1 divided by the number of patch types. In other words, the observed Simpson's Diversity Index divided by the maximum Simpson's Diversity Index for that number of patch types.
(L44) Modified Simpson's Evenness Index
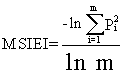
Units: None
Range: 0
£ MSIEI £ 1MSIDI = 0 when the landscape contains only 1 patch (i.e., no diversity) and approaches 0 as the distribution of area among the different patch types becomes increasingly uneven (i.e., dominated by 1 type). MSIDI = 1 when distribution of area among patch types is perfectly even (i.e., proportional abundances are the same).
Description: MSIEI equals minus the logarithm of the sum, across all patch types, of the proportional abundance of each patch type squared, divided by the logarithm of the number of patch types. In other words, the observed modified Simpson's diversity index divided by the maximum modified Simpson's diversity index for that number of patch types.
(L45) Interspersion and Juxtaposition Index
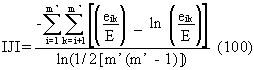
Units: Percent
Range: 0 < IJI
£ 100IJI approaches 0 when the distribution of adjacencies among unique patch types becomes increasingly uneven. IJI = 100 when all patch types are equally adjacent to all other patch types (i.e., maximum interspersion and juxtaposition. IJI is undefined and reported as "NA" in the "basename".full file and a dot "." in the "basename".land file if the number of patch types is less than 3.
Description: IJI equals minus the sum of the length (m) of each unique edge type divided by the total landscape edge (m), multiplied by the logarithm of the same quantity, summed over each unique edge type; divided by the logarithm of the number of patch types times the number of patch types minus 1 divided by 2; multiplied by 100 (to convert to a percentage). In other words, the observed interspersion over the maximum possible interspersion for the given number of patch types. Note, IJI considers all patch types present on an image, including any present in the landscape border, if a border was included. All background edge segments are ignored, as are landscape boundary segments if a border is not provided, because adjacency information for these edge segments is not available.
(L46) Contagion Index
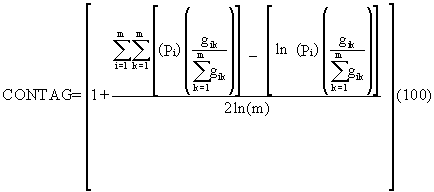
Units: Percent
Range: 0 < CONTAG
£ 100CONTAG approaches 0 when the distribution of adjacencies (at the level of individual cells) among unique patch types becomes increasingly uneven. CONTAG = 100 when all patch types are equally adjacent to all other patch types (i.e., maximum interspersion and juxtaposition. CONTAG is undefined and reported as "NA" in the "basename".full file and a dot "." in the "basename".land file if the number of patch types is less than 2.
Description: CONTAG equals minus the sum of the proportional abundance of each patch type multiplied by number of adjacencies between cells of that patch type and all other patch types, multiplied by the logarithm of the same quantity, summed over each patch type; divided by 2 times the logarithm of the number of patch types; multiplied by 100 (to convert to a percentage). In other words, the observed contagion over the maximum possible contagion for the given number of patch types. Note, CONTAG considers all patch types present on an image, including any present in the landscape border, if present, and considers like adjacencies (i.e., cells of a patch type adjacent to cells of the same type). All background edge segments are ignored, as are landscape boundary segments if a border is not provided, because adjacency information for these edge segments is not available.