Applying Spatial Analysis and Surface Modeling

in Decision-Making Contexts

 

Joseph K. Berry1

Berry & Associates, Suite 300, 2000 South College Avenue, Fort Collins, Colorado 80525
Phone: (970) 215-0825 — E-mail: jberry@innovativegis.com  — Web site: www.innovativegis.com/basis

 

Abstract

 

The characterization of terrain is an important aspect in sound land and resource planning and management.  Many commercial GIS systems provide grid-based analysis tools that can be applied to spatial analysis and surface modeling.  This paper describes several basic procedures for analyzing micro-terrain characteristics: 1) Deviation from Trend, Difference Maps and Deviation Surfaces to identify convex and concave features, 2) Coefficient of Variation Surfaces statistically summarizing disparity in neighboring elevation values, 3) Slope and Aspect Maps that report the magnitude and direction of surface inclination, 3) Slope of a Slope Map (2nd derivative) that summarizes the frequency of the slope changes, and 4) Confluence Maps characterizing the number of uphill locations connected to each surface location.  These tools provide a wealth of different perspectives on surface configuration that are useful in decision-making in a wide variety of geo-based applications.

 

Characterizing Micro-Terrain Features

 

As you look at a landscape you easily see the changes in terrain with some areas bumped up (termed convex) and others pushed down (termed concave).  But how can a computer "see" the same thing?  Since its world is digital, how can the lay of the landscape be transferred into a set of drab numbers? 

 

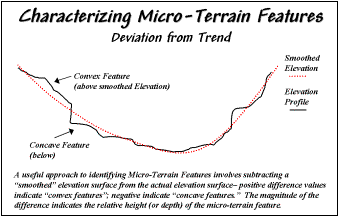Figure 1.  Identifying Convex and Concave features by deviation from the trend of the terrain.

 

One of the most frequently used procedures involves comparing the trend of the surface to the actual elevation values.  Figure 1 shows a terrain profile extending across a small gully.  The dotted line identifies a smoothed curve fitted to the data, similar to a draftsman's alignment of a French curve.  It "splits-the-difference" in the succession of elevation values—half above and half below.  Locations above the trend line identify convex features while locations below identify the concave ones.  The further above or below determines how pronounced the feature is.

 

In a GIS, simple smoothing of the actual elevation values derives the trend of the surface.  The left side of figure 2 shows the actual and smoothed surfaces for a project area.  The flat portion at the extreme left is an area of open water.  The terrain rises sharply from 500 feet to 2500 feet at the top of the hill.  Note the small "saddle" (elevation dips down then up) between the two hilltops.  Also note the small depression in the relatively flat area in the foreground (SW) portion.

 

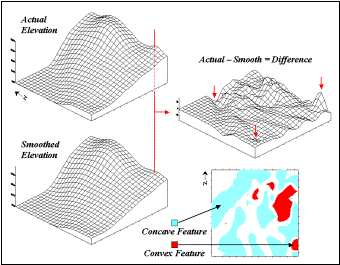Figure 2.  Example of a micro-terrain deviation surface.

 

In generating the smoothed surface, elevation values were averaged for a 4-by-4 window moved throughout the area.  Note the subtle differences between the surfaces—the tendency to pull-down the hilltops and push-up the gullies. 

 

While you see (imagine?) these differences in the surfaces, the computer quantifies them by subtracting.  The difference surface on the right contains values from -84 (prominent concave feature) to +94 (prominent convex feature).  The big bump on the difference surface corresponds to the smaller hilltop on elevation surface.  It's actual elevation is 2016 while the smoothed elevation is 1922 resulting in 2016 - 1922 = +94 difference.  In micro-terrain terms, this area is likely drier that its surroundings as water flows away from it. 

 

The other arrows on the surface indicate other interesting locations.  The "pockmark" in the foreground is a small depression (764 - 796 = -32 difference) that is likely wetter as water flows into it.  The "deep cut" at the opposite end of the difference surface (539 - 623 = -84) suggests a prominent concavity.  However representing the water body as fixed elevation isn't a true account of terra firma configuration and misrepresents the true micro-terrain pattern. 

In fact the entire concave feature in the upper left portion of 2-D representation of the difference surface is suspect due to its treatment of the water body as a constant elevation value.  While a fixed value for water on a topographic map works in traditional mapping contexts it's insufficient in most analytical applications.  Advanced GIS systems treat open water as "null" elevations (unknown) and "mirror" terrain conditions along these artificial edges to better represent the configuration of solid ground.

 

The 2-D map of differences identifies areas that are concave (dark red), convex (light blue) and transition (white portion having only -20 to +20 feet difference between actual and smoothed elevation values).  If it were a map of a farmer's field, the groupings would likely match a lot of the farmer's recollection of crop production—more water in the concave areas, less in the convex areas. 

 

Putting Terrain Information to Use

 

A Colorado dryland wheat farmer knows that some of the best yields are in the lowlands while the uplands tend to "burn-out."  A farmer in Louisiana, on the other hand, likely see things reversed with good yields on the uplands while the lowlands often "flood-out."  In either case, it might make sense to change the seeding rate, hybrid type, and/or fertilization levels within areas of differing micro-terrain conditions. 

 

The idea of variable rate response to spatial conditions has been around for thousands of years as indigenous peoples adjusted the spacing of holes they poked in the ground to drop in a seed and a piece of fish.  While the mechanical and green revolutions enable farmers to cultivate much larger areas they do so in part by applying broad generalizations of micro-terrain and other spatial variables over large areas.  The ability to continuously adjust management actions to unique spatial conditions on expansive tracks of land foretells the next revolution.

 

Investigation of the effects of micro-terrain conditions goes beyond the farm.  For example, the Universal Soil Loss Equation uses "average" conditions, such as stream channel length and slope, dominant soil types and existing land use classes, to predict water runoff and sediment transport from entire watersheds.  These non-spatial models are routinely used to determine the feasibility of spatial activities, such as logging, mining, road building and housing development.  While the procedures might be applicable to typical conditions, they less accurately track unusual conditions clumped throughout an area and provide no spatial guidance within the boundaries of the modeled area. 

 

GIS-based micro-terrain analysis can help us be more like a "modern ancient farmer"— responding to site-specific conditions over large expanses of the landscape.  Calculation of a difference surface simply scratches the surface of micro-terrain analysis. 

 

Some Alternative Approaches

 

The previous section described a technique for characterizing micro-terrain features involving the difference between the actual elevation values and those on a smoothed elevation surface (trend).  Positive values on the difference map indicate areas that "bump-up" while negative values indicate areas that "dip-down" from the general trend in the data. 

 

A related technique to identify the bumps and dips of the terrain involves moving a "roving window" (termed a spatial filter) throughout an elevation surface.  The profile of a gully can have micro-features that dip below its surroundings (termed concave) as shown on the right side of figure 3. 

 

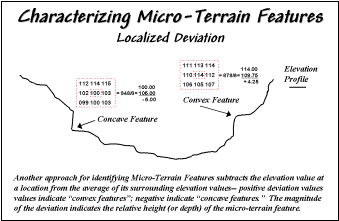Figure 3.  Localized deviation uses a spatial filter to compare a location to its surroundings.

 

The localized deviation within a roving window is calculated by subtracting the average of the surrounding elevations from the center location's elevation.  As depicted in the example calculations for the concave feature, the average elevation of the surroundings is 106, that results in a -6.00 deviation when subtracted from the center's value of 100.  The negative sign denotes a concavity while the magnitude of 6 indicates it's fairly significant dip (a 6/100= .06).  The protrusion above its surroundings (termed a convex feature) shown on the right of the figure has a localized deviation of +4.25 indicating a somewhat pronounced bump (4.25/114= .04). 

 

The result of moving a deviation filter throughout an elevation surface is shown in the top right inset in figure 4.  Its effect is nearly identical to the trend analysis described before-- comparison of each location's actual elevation to the typical elevation (trend) in its vicinity.  Interpretation of a Deviation Surface is the same as that for the difference surface—protrusions (large positive values) locate drier convex areas; depressions (large negative values) locate wetter concave areas.

 

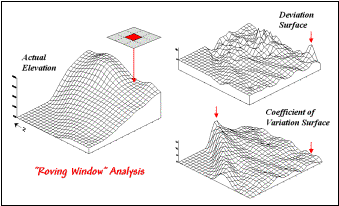Figure 4.  Applying Deviation and Coefficient of Variation filters to an elevation surface.

 

The implication of the "Localized Deviation" approach goes far beyond simply an alternative procedure for calculating terrain irregularities.  The use of "roving windows" provides a host of new metrics and map surfaces for assessing micro-terrain characteristics.  For example, consider the Coefficient of Variation (Coffvar) Surface shown in the bottom-right portion of figure 4.  In this instance, the standard deviation of the window is compared to its average elevation—small "coffvar" values indicate areas with minimal differences in elevation; large values indicate areas with lots of different elevations.  The large ridge in the coffvar surface in the figure occurs along the shoreline of a lake.  Note that the ridge is largest for the steeply-rising terrain with big changes in elevation.  The other bumps of surface variability noted in the figure indicate areas of less terrain variation.

 

While a statistical summary of elevation values is useful as a general indicator of surface variation or "roughness," it doesn't consider the pattern of the differences.  A checkerboard pattern of alternating higher and lower values (very rough) cannot be distinguished from one in which all of the higher values are in one portion of the window and lower values in another. 

 

There are several roving window operations that track the spatial arrangement of the elevation values as well as aggregate statistics.  A frequently used one is terrain slope that calculates the "slant" of a surface.  In mathematical terms, slope equals the difference in elevation (termed the "rise") divided by the horizontal distance (termed the "run"). 

 

As shown in figure 5, there are eight surrounding elevation values in a 3x3 roving window.  An individual slope from the center cell can be calculated for each one.  For example, the percent slope to the north (top of the window) is ((2332 - 2262) / 328) * 100 = 21.3%.  The numerator computes the rise while the denominator of 328 feet is the distance between the centers of the two cells.  The calculations for the northeast slope is ((2420 - 2262) / 464) * 100 = 34.1%, where the run is increased to account for the diagonal distance (328 * 1.414 = 464). 

 

The eight slope values can be used to identify the Maximum, the Minimum and the Average slope as reported in the figure.  Note that the large difference between the maximum and minimum slope (53 - 7 = 46) suggests that the overall slope is fairly variable.  Also note that the sign of the slope value indicates the direction of surface flow—positive slopes indicate flows into the center cell while negative ones indicate flows out.  While the flow into the center cell depends on the uphill conditions (we'll worry about that in a subsequent section), the flow away from the cell will take the steepest downhill slope (southwest flow in the example… you do the math).

 

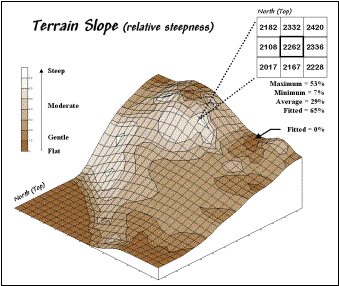Figure 5.  Calculation of slope considers the arrangement and magnitude of elevation differences within a roving window.

 

In practice, the "average slope" can be misleading.  It is supposed to indicate the overall slope within the window but fails to account for the spatial arrangement of the slope values.  An alternative technique "fits a plane" to the nine individual elevation values.  The procedure determines the best fitting plane by minimizing the deviations from the plane to the elevation values.  In the example, the Fitted slope is 65%… more than the maximum individual slope.  At first this might seem a bit fishy—overall slope more than the maximum slope—but believe me, determination of fitted slope is a different kettle of fish than simply scrutinizing the individual slopes. 

 

Numerical Analysis and Surface Modeling

 

The previous sections have presented several techniques for generating maps that identify the bumps (convex features), the dips (concave features) and the tilt (slope) of a terrain surface.   Although the procedures have a wealth of practical applications, the underlying hidden agenda of the discussion is to get you thinking of geographic space in a less traditional way—as an organized set of numbers (numerical data), instead of points, lines and areas represented by various colors and patterns (graphic map features). 

 

A terrain surface is organized as a rectangular "analysis grid" with each cell containing an elevation value.  Grid-based processing involves retrieving values from one or more of these "input data layers" and performing a mathematical or statistical operation on the subset of data to produce a new set numbers.  While computer mapping or spatial database management often operates with the numbers defining a map, these types of processing simply repackage the existing information.  A spatial query to "identify all the locations above 8000' elevation in El Dorado County" is a good example of a repackaging interrogation.  

 

Map analysis operations, on the other hand, create entirely new spatial information.  For example, a map of terrain slope can be derived from an elevation surface, then used to expand the geo-query to "identify all the locations above 8000' elevation in El Dorado County (existing data) that exceed 30% slope (derived data)."  While the discussion in this series of columns focuses on applications in terrain analysis, the subliminal message is much broader—map analysis procedures derive new spatial information from existing information. 

 

Further Consideration of Slope

 

Now back to the business of characterizing map surfaces.  The previous discussions described several approaches for calculating terrain slope from an elevation surface.  Each of the approaches used a "3x3 roving window" to retrieve a subset of data, yet applied a different analysis function (maximum, minimum, average or "fitted" summary of the data). 

 

Figure 6 shows the slope map derived by "fitting a plane" to the nine elevation values surrounding each map location.  The inset in the upper left corner of the figure shows a 2-D display of the slope map.  Note that steeper locations primarily occur in the upper central portion of the area, while gentle slopes are concentrated along the left side.

 

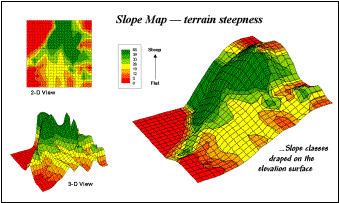Figure 6. 2-D, 3-D and draped displays of terrain slope.

 

The inset on the right shows the elevation data as a wire-frame plot with the slope map draped over the surface.  Note the alignment of the slope classes with the surface configuration—flat slopes where it looks flat; steep slopes where it looks steep. 

 

The 3-D view of slope in the lower left, however, looks a bit strange.  The big bumps on this surface identify steep areas with large slope values.  The ups-and-downs (undulations) are particularly interesting.  If the area was perfectly flat, the slope value would be zero everywhere and the 3-D view would be flat as well.  But what do you think the 3-D view would look like if the surface formed a steeply sloping plane?

 

Are you sure?  The slope values at each location would be the same, say 65% slope, therefore the 3-D view would be a flat plane "floating" at a height of 65.  That suggests a useful principle—as a slope map progresses from a constant plane (single value everywhere) to more ups-and-downs (bunches of different values), an increase in terrain roughness is indicated. 

 

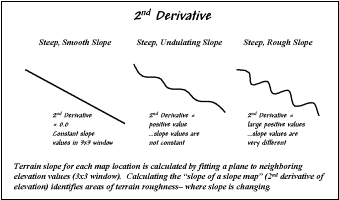Figure 7.  Assessing terrain roughness through the 2nd derivative of an elevation surface.

 

Figure 7 outlines this concept by diagramming the profiles of three different terrain cross-sections.  An elevation surface's 2nd derivative (slope of a slope map) quantifies the amount of ups-and-downs of the terrain.  For the straight line on the left, the "rate of change in elevation per unit distance" is constant with the same difference in elevation everywhere along the line—slope = 65% everywhere.  The resultant slope map would have the value 65 stored at each grid cell, therefore the "rate of change in slope" is zero everywhere along the line (no change in slope)—slope2 = 0% everywhere. 

 

A slope2 value of zero is interpreted as a perfectly smooth condition, which in this case happens to be steep.  The other profiles on the right have varying slopes along the line, therefore the "rate of change in slope" will produce increasing larger slope2 values as the differences in slope become increasingly larger.

 

So who cares?  Water drops for one, as steep smooth areas are ideal for downhill racing, while "steep 'n rough terrain" encourages more infiltration, with "gentle yet rough terrain" the most. 

 

Figure 8 shows a roughness map based on the 2nd derivative for the same terrain as depicted in Figure 6.  Note the relationships between the two figures.  The areas with the most "ups-and-downs" on the slope map in figure 6 correspond to the areas of highest values on the roughness map in figure 8. 

 

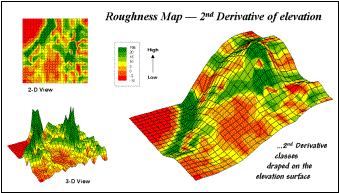Figure 8.  2-D, 3-D and draped displays of terrain roughness.

 

Now focus your attention on the large steep area in the upper central portion of the map.  Note the roughness differences for the same area as indicated in figure 8—the favorite raindrop racing areas are the smooth portions of the steep terrain occurring along the central portion of the front face of the hill. 

 

Mapping Water Confluence

 

The preceding section focused on terrain steepness and roughness.  While the concepts are simple and straightforward, the mechanics of computing them are a bit more challenging.  As you hike in the mountains your legs sense the steepness and your mind is constantly assessing terrain roughness.  A smooth, steeply-sloped area would have you clinging to things while a rough steeply-sloped area would look more like stair steps.

 

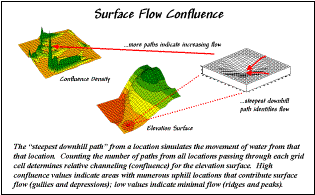Figure 9.  Map of surface flow confluence.

 

Water has a similar vantage point of the slopes it encounters, except given its head, water will take the steepest downhill path, sort of like an out-of-control skier.  Figure 9 shows a map of surface flow confluence.  It is based on the assumption that water will follow a path that chooses the steepest downhill step at each point (grid cell) along the terrain surface.  In effect, a drop of water is placed at each location and allowed to pick its path down the terrain surface.  Each grid cell that is traversed gets the value one added to it.   As the paths from other locations are considered the areas sharing common paths get increasing larger values. 

 

The inset on the right shows the path taken by a couple of drops into a slight depression.  The inset on the left shows the considerable inflow for the depression as a high peak in the 3-D display.  The high value indicates that a lot of uphill locations are connected to this feature.  However, note that the pathways to the depression are concentrated along the southern edge of the area.

 

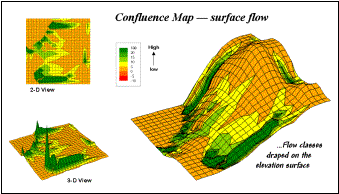Figure 10.  2-D, 3-D and draped displays of surface flow confluence.

 

Ridges on the confluence density surface identify areas of high surface flow.  In figure 10, note how these areas (darker) align with the creases in the terrain as shown on the draped elevation surface on the right.  The 2-D map provides a more familiar map rendering of where not to unroll your sleeping bag if flash floods are likely.

 

Putting It All Together

 

The various spatial analysis techniques for characterizing terrain surfaces provide a wealth of different perspectives on surface configuration.  Deviation from Trend, Difference Maps and Deviation Surfaces are used to identify areas that "bump-up" (convex) or "dip-down" (concave).  A Coefficient of Variation Surface looks at the overall disparity in elevation values occurring within a small area.  A Slope Map shares a similar algorithm (roving window) but the summary of is different and reports the "tilt" of the surface.  An Aspect Map extends the analysis to include the direction of the tilt as well as the magnitude.  The Slope of a Slope Map (2nd derivative) summarizes the frequency of the changes along an incline and reports the roughness throughout an elevation surface.  Finally, a Confluence Map takes an extended view and characterizes the number of uphill locations connected to each location. 

 

The coincidence of these varied perspectives can provide valuable input to decision-making.  Areas that are smooth, steep and coincide with high confluence are strong candidates for gully-washers that gouge the landscape.  On the other hand, areas that are rough, gently-sloped and with minimal confluence are relatively stable.  Concave features in these areas tend to trap water and recharge soil moisture and the water table.  Convex features under erosive conditions tend to become more prominent as the confluence of water flows around it.

 

Similar interpretations can be made for hikers, who like raindrops react to surface configuration in interesting ways.  While steep, smooth surfaces are avoided by all but the rock-climber, too gentle surfaces tend too provide boring hikes.  Prominent convex features can make interesting areas for viewing—from the top for hearty and from the bottom for the aesthetically bent.  Areas of water confluence don't mix with hiking trail unless a considerable number of water-bars are placed in the trail. 

 

While these "rules-of-thumb" make sense in a lot of circumstances, there are numerous exceptions that undercut them.  Two concerns are particularly important.  First, conditions along the surface can alter the effect of terrain characteristics.  For example, soil properties and vegetation present greatly effect surface runoff and sediment transport.  The nature of accumulated distance along the surface

 

In addition, the resolution of the elevation grid can effect the calculations.  In the case of water drops the gridding resolution must be high to capture the subtle twists and bends that direct water flow.  A hiker on the other hand, is less sensitive to subtle changes in elevation.  The rub is that collection of the appropriate elevation is prohibitive in most practical applications.  The result is that existing elevation data, such as the USGS Digital Terrain Models (DTM), are used in most cases.  Since the GIS procedures are independent of the gridding resolution, inappropriate maps can be generated and used in decision-making.  The recognition of the importance of spatial analysis and surface modeling is imperative.  Its effective use requires informed and wary users.

 

_____________________________________

 

Author's Note:  This paper is based on a series of "Beyond Mapping" columns on characterizing micro-terrain appearing in GeoWorld magazine, January through April, 2000.  The calculations and displays using MAPcalc software by Red Hen Systems, Inc., 2310 East Prospect Road, Suit A, Fort Collins, USA 80525, (800) 237-4182, Email: info@redhensystems.com, Web site: http://www.redhensystems.com/

1 Joseph K. Berry is President of Berry & Associates // Spatial Information Systems, Inc., consultants and software developers in GIS technology.