Beyond Mapping III
|
Map
Analysis book with companion CD-ROM for hands-on exercises and further reading |
GIS Data Are Rarely
Normal — describes
the basic non-spatial descriptive statistics
Unlocking the Keystone
Concept of Spatial Dependency
— discusses spatial
dependency and illustrates the effects of different spatial arrangements of the
same set of data
Measuring
Spatial Dependency — describes
the basic measures of autocorrelation
Extending
Spatial Dependency to Maps — describes
a technique for generating a map of spatial autocorrelation
Use Polar Variograms
to Assess Distance and Direction Dependencies —
discuses a procedure to incorporate direction as well as distance for assessing
spatial dependency
Note: The processing and figures discussed in this topic were derived using MapCalcTM
software. See www.innovativegis.com to download a
free MapCalc Learner version with tutorial materials for classroom and
self-learning map analysis concepts and procedures.
<Click here> right-click to download a printer-friendly
version of this topic (.pdf).
(Back to the Table of Contents)
______________________________
(GeoWorld, October 1998, pg. 24-26)
Most of us are familiar with the old “bell-curve” for school
grades. You know, with lots of C’s,
fewer B’s and D’s, and a truly select set of A’s and F’s. Its shape is a perfect bell, symmetrical
about the center with the tails smoothly falling off toward less frequent
conditions.
Although the distribution is familiar and easy to visualize,
the normal
distribution (bell-shaped) isn’t as normal (typical) as you might
think. For example, Newsweek recently noted that the average
grade at a major ivy-league university isn’t a solid C with a few A’s and F’s
sprinkled about as you might imagine, but an A- with a lot of A’s trailing off
to lesser amounts of B’s, C’s and (heaven forbid) the rare D’s and F’s.
The frequency distributions of mapped data also tend toward the ab-normal (formally termed asymmetrical). For example, consider the elevation data
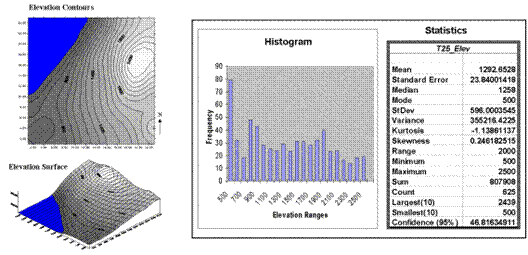
shown in figure 1. The
contour map and 3-D surface on the left depict the geographic distribution of
the data. Note the distinct pattern
of the terrain with higher elevations in the northeast and lower ones along the
western portion. As is normally the case
with mapped data, the elevation values are neither uniformly nor randomly
distributed in
geographic space. The
unique pattern is the result complex physical processes driven by a host of
factors—not spurious, arbitrary, constant or even “normal” events.
Figure 1. Mapped data are characterized by their geographic distribution (maps on the left) and their numeric distribution (histogram and statistics on the right).
Now turn your attention to the numeric distribution of the
data depicted in the right side of the figure.
The data view was generated by simply transferring the gridded
elevation values to Excel, then applying the Histogram and Descriptive
Statistics options of the Data Analysis add-in tools. The mechanics used to
plot the histogram and generate the statistics were a piece-of-cake, but the
real challenge is to make some sense of it all.
Note that the data aren’t distributed as a normal bell-curve, but appear
flattened and slightly shifted to the left.
The tall spike at the lowest elevation range (500-600 feet) is due to
the lake in the northwest corner. If the
lake was drained (or its bathometry considered) some of the spike’s values
would be assigned smaller elevations and the distribution would broaden and flatten
even more.
If the terrain contained a plateau or mesa instead of the smooth hill in the
northeast, there would be a spike at the high end of the histogram. What do you think the histogram would look
like if the area contained several chimney-rocks or “whoodoos”
scattered about a flat plain? Or if the area were centered on an escarpment?
The mental exercise linking geographic
space with data space is a good one, and some general points ought to be
noted. First, there isn’t a fixed
relationship between the two views of the data’s distribution (geographic and
data). A myriad of geographic patterns
can result in the same histogram. That’s
because spatial data contains additional information—where, as well as what—and
the same data summary of the “what’s” can reflect a multitude of spatial
arrangements (“where’s).
But is the reverse true? Can a given
geographic arrangement result in different data views? Nope, and it’s this relationship that
catapults mapping and geo-query into the arena of mapped data analysis. Traditional analysis techniques assume a
functional form for the frequency distribution (histogram shape), with the
standard normal (bell-shaped) being the most prevalent. Last June’s column described the basic
descriptive statistics Excel’s summary table— maximum, minimum, range, mode, median, mean (average), variance,
standard deviation and an additional one termed coefficient of variation.
The discussion described how these statistics portray the central
tendency (typical condition) of a data set.
In effect, they reduce the complexity of a large number of measurements
to just a handful of numbers and provide a foothold for further analysis.
A brief discussion of the additional indices in Excel’s table is
warranted. The sum and the count
should be obvious—the total of all the measurements (sum= 807,908 “total” feet
above sea level doesn’t mean much in this context) and the number of
measurements (count= 625 data values indicates a fairly big data set as
traditional statistics go, but fairly small for spatial statistics). The largest/smallest statistic in the
table identifies the average of a user-specified number of values (10 in this
case) at the extreme ends of the data set.
It is interesting to note that the average of the 10 smallest elevation
values (500) is the same as the minimum value, while the average of the 10
largest values (2439) is well below the maximum value of 2500.
The standard
error calculates the average difference between the individual data
values and the mean (StdError= sum [[x-mean]**2] / [n*[n-1]]).
If the average deviation is fairly small, then the mean is fairly close
to each of the sample measurements. The
standard error for the elevation data is 23.84001418 (whoa Excel, way too many
decimals—nothing in statistics is that precise). The statistic means that the mean is on the
average (got that?) about 24 feet above or below the 625 individual elevation
values comprising the map. Useful
information, but often the attention of most
The confidence
level is a range on either side of a sample mean that you are fairly
sure contains the population (true) average. For example, if you have some data
on mail order delivery times, you can determine, with a particular level of
confidence (usually 95%), the earliest and latest a product will likely arrive.
The elevation data’s confidence value of 46.81634911 suggests that we can be fairly sure that the “true” average
elevation is between 1245 and 1340. But
this has a couple of important assumptions—that the data represents a good
sample and that the normal curve is a good representation of the actual
distribution.
But what if the distribution isn’t normal?
What if it is just a little ab-normal? What if it
is a lot? That’s the stuff of doctoral
theses, but there are some general considerations that ought to be noted. First, there are some important statistics
that provide insight into how normal a data set is. Skewness tells us if the data is
lop-sided. Formally speaking, it
“characterizes the degree of asymmetry of a distribution around its mean.”
Positive skewness indicates a distribution shifted to left, while negative
skewness indicates a shift to the right and 0 skewness
is indicates perfectly symmetrical data.
The larger the value, the more pronounced is the lop-sided shift. In the elevation data, a skewness value of
.246182515 indicates a slight shift to the right.
Another measure of ab-normality
is termed kurtosis. It
characterizes the relative “peakedness or flatness”
of a distribution compared with the “ideal” bell-shaped distribution. A
positive kurtosis indicates a relatively peaked distribution, while a negative
kurtosis indicates a relatively flat one and 0 is just the right amount (sounds
like Goldilock’s “papa, mamma and baby bear” sizing
of distribution shape). Its magnitude
reports the degree of distortion from a perfect bell-shape. The –1.13861137 kurtosis value for the elevation
data denotes a substantial flattening.
All in all, the skewness and kurtosis values don’t bode well for the elevation
data being normally distributed. In
fact, a lot of spatial data isn’t very normal…some might say most. So what do you do? Throw away the Excel-type descriptive
statistics? Punt on statistical analysis
and simply generate really cool graphics for visceral visions of the
relationships? Do you blindly go ahead
and impose assumptions of normalcy just to force-fit
normal analysis procedures? Good
questions, but they will have to wait for the next section’s discussions.
Unlocking the Keystone Concept of Spatial Dependency
(GeoWorld, November 1998, pg. 28-30)
The previous section investigated the numerical character of
a gridded elevation surface. Keystone to
the discussion was the degree of “normality” exhibited in the data as measured
by commonly used descriptive statistics— min,
max, range, median, mode, mean (or average), variance, standard deviation,
standard error, confidence level, skewness and kurtosis. All in all, it appeared that the elevation
data didn’t fit the old “bell-shaped” curve very well.
So, how useful is “normal” statistics in
At the risk of overstepping my bounds of expertise, let me suggest that using
the average to represent the central tendency of a data set is usually OK. However, when the data isn’t normally
distributed the average might not be a good estimator of the “typical”
condition. Similarly, the standard
deviation can be an ineffective measure of dispersion for ab-normally distributed data… it all depends.
So, what’s a
Even more disturbing, however, is the
realization that while descriptive statistics might provide insight into the
numerical distribution of the data, they provide no information what-so-ever
into the spatial distribution of the data.
As noted last month, all sorts of terrain configurations can produce
exactly the same set of descriptive statistics.
That’s because traditional measures are breed to ignore geographic
patterns— in fact spatial independence is an underlying assumption.
So how can one tell if there is spatial dependency locked inside a data
set? You know, Tobler’s first law of geography that “all things are
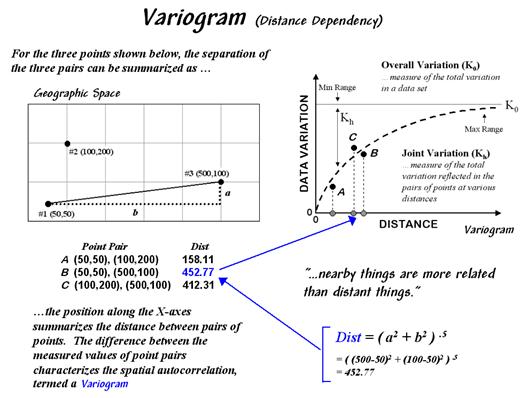
related but nearby things are more related than distant things.” Let’s use Excel* and some common sense to
investigate this keystone concept and the approach used in deriving a
descriptive statistics that tracks spatial dependency.
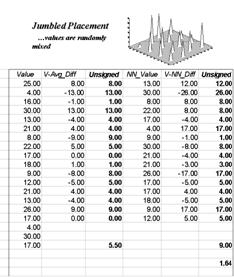
The left side of the figure 1 identifies sixteen sample points in a 25 column
by 25 row analysis grid (origin at 1, 1 in the upper left, northwest
corner). The positioning of the samples are depicted in the two 3-D plots. Note that the sample positions are the same
(horizontal axes), only the measurements at each location vary (vertical
axis). The plot on the left depicts
sample values that form a plane constantly increasing from the southwest to the
northeast. The plot on the right depicts
a jumbled arrangement of the same measurement values.
Figure
1. The spatial dependency
in a data set compares the “typical” and “nearest neighbor” differences— if the
nearest neighbor differences are less than the typical differences, then
"nearby things are more similar than distant things."
The first column (labeled Value) in the Tilted and Jumbled
worksheets confirm that the traditional descriptive statistics are identical—
derived from same values, just in different positions. The second column calculates the difference
between each value and the average of the entire set of samples. The sign of the difference indicates whether
the value is above or below the average, or typical value. The third column (labeled Unsigned) identifies the magnitude of
the difference by taking its absolute value— |Value – Average|. The average of all the unsigned differences
summarizes the “typical” difference. The
relatively large figure of 5.50 for both the Tilted and Jumbled data sets
establishes that the individual samples aren’t very similar overall.
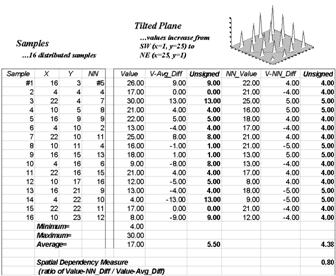
The next three columns in both worksheets provide insight into the spatial
dependency in the two data sets by evaluating Tobler’s
first law. The NN_Value column identifies the
value for the nearest neighboring (closest) sample. It is determined by solving for the distance
from each sample location to all of the others using the Pythagorean theorem (c2= a2 + b2), then
assigning the measurement value of the closest sample. The final two columns calculate the unsigned
difference between the value at a location and its
nearest neighboring value, then compute the unsigned difference— |Value
– NN_Value|. Note that the Tilted data’s nearest neighbor
difference (4.38) is considerably less than that for the Jumbled data
(9.00).
Now the stage is set. If the nearest
neighbor differences are less than the typical differences, then “…nearby
things are more related than distant things.”
A simple Spatial Dependency Measure is calculated as the ratio of the
two differences. If the measure is 1.0,
then minimal spatial dependency exists.
As the measure gets smaller, increased positive spatial dependency is
indicated; as it gets larger, increased negative spatial dependency is
indicated (nearby things are less similar than distant things).
OK, so what if the basic set of descriptive statistics can be extended to
include a measure of spatial dependency?
What does it tell you? How can
you use it? Its basic interpretation is
to what degree the data forms a discernable spatial pattern. If spatial dependency is minimal or negative
there is little chance that geographic space can be used to explain the
variation in the data. In these
conditions, assigning the average (or median) to an entire polygon is warranted. On the other hand, if strong positive spatial
dependency is indicated, you might consider subdividing the polygon into more
homogenous parcels to better “map the variation” locked in a data set. Or better yet, treat the area as a continuous
surface (gridded data). But further
discussion of refinements in calculating and interpreting spatial dependency
must be postponed until next time.
_____________________________
*Note: the Excel worksheets supporting the discussions of the Tilted and Jumbled data sets (as well as a Blocked and a Random pattern) can be downloaded from the “Column Supplements” page at www.innovativegis.com/basis.
(GeoWorld, December 1998, pg. 28)
Recall last month's discussion of
"nearest neighbor" spatial dependency to test the assertion that
"nearby things are more related than distant things." The procedure was simple—calculate the
difference between each sample value and its closest neighbor (|Value - NN_Value|), then compare them to the differences based on
the typical condition (|Value - Average|).
If the Nearest Neighbor and Average differences are about the same,
little spatial dependency exists. If the
nearby differences are substantially smaller than the typical differences, then
strong positive spatial dependency is indicated and it is safe to assume that nearby
things are more related.
But just how are they related? And just
how far is "nearby?" To answer
these questions the procedure needs to be expanded to include the differences
at the various distances separating the samples. As with the previous discussions, Excel can
be used to investigate these relationships.*
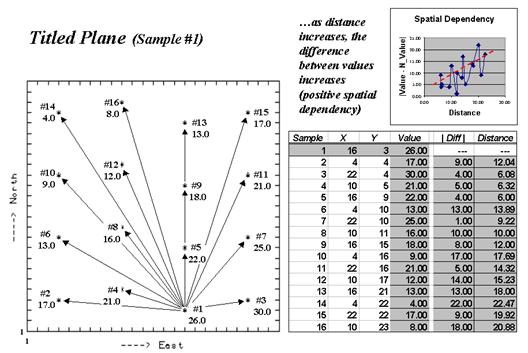
The plot on the left side of Figure 1, identifies the positioning and
sample values for the Tilted Plane data set described last month.
Figure 1. Spatial dependency as a function of distance for sample point #1.
The arrows emanating from sample #1 shows its
15 paired values. The table on the right
summarizes the unsigned differences (|Diff
|) and distances (Distance) for
each pair. Note that the
"nearby" differences (e.g., #3= 4.0, #4= 5.0 and #5= 4.0) tend to be
much smaller than the "distant" differences (e.g., #10= 17.0, #14=
22.0, and #16= 18.0). The graph in the
upper right portion of the figure plots the relationship of sample differences
versus increasing distances. The dotted
line shows a trend of increasing differences (a.k.a. dissimilarity) with
increasing distances.
Now imagine calculating the differences for all the sample pairs in the data
set—the 16 sample points combine for 120 sample pairs—(N*(N-1)/2)= (16*15)/2=
120). Admittedly, these calculations
bring humans to their knees, but it's just a microsecond or so for a computer. The result is a table containing the |Diff |
and Distance values for all of the sample pairs.
The extended table embodies a lot of information for assessing spatial
dependency. The first step is to divide
the samples into two groups— close and distant pairs. For consistency across data sets, let's
define the "breakpoint" as a proportion of the maximum distance (Dmax)
between sample pairs. Figure 2 shows the
results of applying a dozen breakpoints to divide the data set into
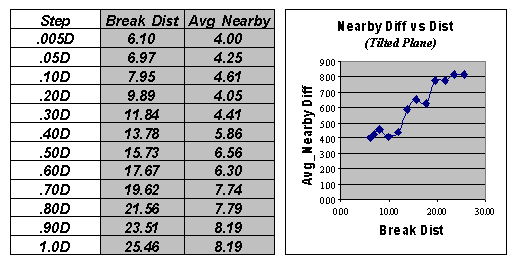
"nearby" and "distant" sample sets. The first row in the table identifies very
close neighbors (.005Dmax= 6.10) and calculates the average nearby
differences (|Avg_Nearby|) as 4.00. The remaining rows in the table track the
differences for increasing distances defining nearby samples. Note that as neighborhood size increases, the
average difference between sample values increases. For this data set, the greatest difference
occurs for the neighborhood that captures all of the data (1.00Dmax=
25.46 with an average difference of 8.19).
Figure 2. Average “nearby” differences for increasing breakpoint distances used to define neighboring samples.
The techy-types
among us will note that the plot of “Nearby Diff vs. Dist” in Figure 28-4 is
similar to that of a variogram. Both assess the difference among sample
values as a function of distance.
However, the variogram tracks the difference at discrete distances,
while the “Nearby Diff vs Dist” plot considers all of
the samples within increasingly larger neighborhoods.
This difference in approach
allows us to directly assess the essence of spatial dependency—whether “nearby
things are more related than distant things.”
A distance-based spatial dependency
measure (SD_D) can be calculated as— SD_D = [|Avg_Distant|
- |Avg_Nearby|] / |Avg_Distant|.
The effect of this processing is like passing
a donut over the data. When centered on
a sample location, the “hole” identifies nearby samples, while the “dough” determines
distant ones. The “hole” gets
progressively larger with increasing breakpoint distances. If, at a particular step, the nearby samples
are more related (smaller |Avg_Nearby| differences)
than the distant set of samples (larger |Avg_Distant|
differences), positive spatial dependency is indicated.
Figure 3. Comparing spatial dependency by directly assessing differences of a sample’s value to those within nearby and distant sets.
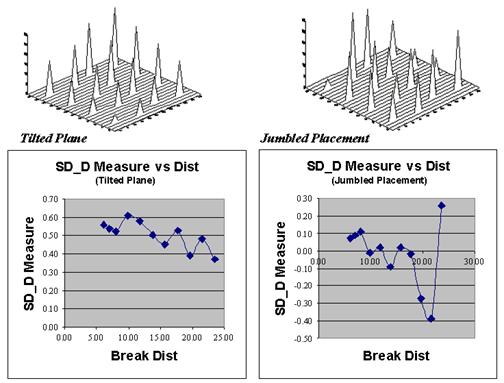
Now let’s put the SD_D measure to use. Figure 28-5 plots the measure for the Tilted
Plane (TP with constantly increasing values) and Jumbled Placement (JP with a
jumbled arrangement of the same values) sample sets used last month. First notice that the measures for TP are
positive for all breakpoint distances (nearby things are always more related),
whereas they bounce around zero for the JP pattern. Next, notice the magnitudes of the measures—
fairly large for TP (big differences between nearby and distant similarities);
fairly small for JP. Finally, notice the
trend in the plots—downward for TP (declining advantage for nearby neighbors);
flat, or unpredictable for JP.
So what does all this tell us? If the
sign, magnitude and trend of the SD_D measures are like TP’s, then positive
spatial dependency is indicated and the data conforms to the underlying
assumption of most spatial interpolation techniques. If the data is more like JP, then “interpolator beware.”
_____________________________
*Note: the Excel worksheets supporting the discussion of the Tilted and Jumbled data sets (as well as a Blocked and Random pattern) can be downloaded from the “Column Supplements” page at www.innovativegis.com/basis.
Extending Spatial Dependency to
Maps
(GeoWorld, January 1999, pg. 26-27)
The past three columns have focused on the important
geographical concept of spatial dependency— that nearby things are more related
than distant things. The discussion to
date has involved sets of discrete sample points taken from a variety of
geographic distributions. Several
techniques were described to generate indices tracking the degree of spatial
dependency in point sampled data.
Now let’s turn our attention to continuously mapped data, such as satellite
imagery, soil electric conductivity, crop yield or
product sales surfaces. In these
instances, a grid data structure is used and a value is assigned to each cell
based on the condition or character at that location. The result is a set of data that continuously
describes a mapped variable. These data are radically different from point
sampled data as they fully capture the spatial relationships throughout an
entire area.
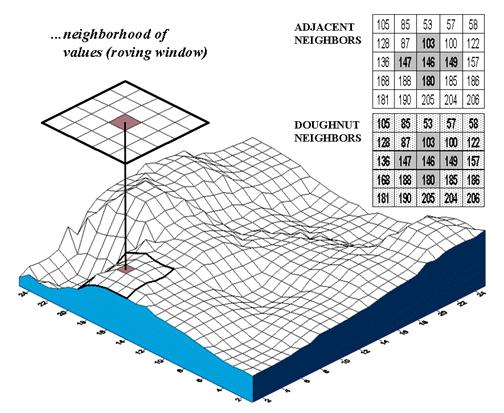
Figure 1. Spatial dependency in continuously mapped data involves summarizing the data values within a “roving window” that is moved throughout a map.
The analysis techniques for spatial
dependency in these data involve moving a “roving window” throughout the data
grid. As depicted in figure 1, an
instantaneous moment in the processing establishes a set of neighboring cells
about a map location. The map values for
the center cell and its neighbors are retrieved from storage and depending on
the technique, the values are summarized.
The window is shifted so it centers over the next cell and the process
is repeated until all map locations have been evaluated. Various methods are used to deal with
incomplete windows occurring along map edges and areas of missing data.
The configuration of the window and the
summary technique is what differentiates the various spatial dependency
measures. All of them, however, involve
assessing differences between map values and their relative geographic
positions. In the context of the data
grid, if two cells are close together and have similar values they are
considered spatially related; if their values are different, they are
considered unrelated, or even negatively related.
Geary’s C and Moran’s I, introduced in the 1950’s, are the most frequently used
measures for determining spatial autocorrelation in mapped data. Although the equations are a bit
intimidating—
Geary’s C = [(n –1) SUM wij (xi – xj)2] / [(2 SUM wij) SUM (xi – m)2]
Moran’s I = [n SUM wij (xi – m) (xj – m)] / [(SUM wij) SUM (xi – m)2]
where, n = number of cells in the grid
m = the mean of the values in
the grid
xi = value of cell
in group i and xj
= value of cell in group j
wij
= a switch set to 1 if the cells are adjacent; 0 if not adjacent (diagonal)
—the underlying concept is fairly
simple.
For example, Geary’s C simply compares the squared differences in values
between the center cell and its adjacent neighbors (numerator tracking “xi
– xj”) to the overall difference based on
the mean of all the values (denominator tracking “xi – m”). If the adjacent differences are less, then
things are positively related (similar, clustered). If they are more, then things are negatively
related (dissimilar, checkerboard). And
if the adjacent differences are about the same, then things are unrelated
(independent, random). Moran’s I is a similar measure, but relates the product of the
adjacent differences to the overall difference.
Now let’s do some numbers. An adjacent neighborhood consists of the
four contiguous cells about a center cell, as highlighted in the upper right
inset of figure 1. Given that the mean
for all of the values across the map is 170, the essence for this piece of
Geary’s puzzle is
C = [(146-147)2 + (146-103) 2 + (146-149)
2 + (146-180) 2] / [4 * (146-170) 2]
= [ 1 + 1849 + 9 + 1156 ] / [ 4 *
576 ] = 3015 /2304 = 1.309
Since the Geary’s C ratio is just a bit
more than 1.0, a slightly uncorrelated spatial dependency is indicated for this
location. As the window completes its
pass over all of the other cells, it keeps a running sum of the numerator and
denominator terms at each location. The
final step applies some aggregation adjustments (the “eye of newt” parts of the
nasty equation) to calculate a single measure encapsulating spatial
autocorrelation over the whole map— a Geary’s C of 0.060 and a Moran’s I of
0.943 for the map surface shown in figure 1.
Both measures report strong positive autocorrelation for the mapped
data. The general interpretation of the
C and I statistics can be summarized as follows.
|
0 < C < 1 |
Strong positive autocorrelation |
I > 0 |
|
C > 1 |
Strong Negative autocorrelation |
I < 0 |
|
C = 1 |
Random distribution of values |
I = 0 |
In the tradition of good science, let me suggest
a new, related measure—
Although this new measure might be intuitive—adjacent differences (nearby
things) versus overall difference (distant things)—it’s much too ugly for
statistical canonization. First, the
values are too volatile and aren’t constrained to an easily interpreted
range. More importantly, the measure
doesn’t directly address “localized spatial autocorrelation” because the nearby
differences are compared to distant differences represented as the map mean.
That’s where the doughnut neighborhood
comes in. The roving window is divided
into two sets of data—the adjacent values (inside ring of nearby things) and
the doughnut values (outside ring of distant things). One could calculate the mean for the doughnut
values and substitute it for Geary’s C’s denominator. But since there’s just a few numbers in the
outer ring, why not use the actual variation between the center and each
doughnut value? That directly assesses whether
nearby things are more related than distant things for each map neighborhood. A user can redefine “distant things” simply
by changing the size of the window. In
fact, if you recall last month’s article, a series of window sizes could be
evaluated and differences between the maps at various “doughnut radii” could
provide information about the geographic sensitivity of spatial dependency
throughout the mapped area (sort of a mapped variogram).
But let’s take the approach one step further for a new measure we might call Berry IT (yep, you got it… "bury it" for tracking the Intimidating Territorial
autocorrelation). Such a measure is
reserved for the statistically adept as it performs an F-test for significant
difference between the adjacent and doughnut data groups for each neighborhood. Check out this month’s Column Supplement for
more info and an Excel worksheet applying several concepts for mapping spatial dependency.
Use Polar Variograms to Assess Distance and Direction
Dependencies
(GeoWorld, September 2001, pg. 24)
The previous columns have investigated spatial dependency—the
assumption that “nearby things are more related than distant things.” This autocorrelation forms the basic concept
behind spatial interpolation and the ability to generate maps from point sampled
data. If there is a lot of spatial
autocorrelation in a set of samples, expect a good map; if not, expect a map of
pure, dense gibberish.
An index of spatial autocorrelation compares the differences between nearby sample pairs with those from the average of the entire data set. One would expect a sample point to be more like its neighbor than it is to the overall average. The larger the disparity between the nearby and average figures the greater the spatial dependency and the likelihood of a good interpolated map.
A variogram plot takes the investigation a bit
farther by relating the similarity among samples to the array of distances
between them. Figure 1 outlines the
mechanics and important aspects of the relationship. The distance between a pair of points is
calculated by the Pythagorean theorem and plotted along the X-axis. A normalized difference between sample values
(termed semi-variance) is calculated and plotted along the Y-axis. Each point-pair is plotted and the pattern of
the points analyzed.
Figure
1. A variogram relates the
difference between sample values and their distance.
Spatial autocorrelation exists if the differences between
sample values systematically increase as the distances between sample points
becomes larger. The shape and
consistency of the pattern of points in the plot characterize the degree of
similarity. In the figure, an idealized
upward curve is indicated. If the
remaining point-pairs continue to be tightly clustered about the curve
considerable spatial autocorrelation is indicated. If they are scattered throughout the plot
without forming a recognizable pattern, minimal autocorrelation is
present.
The “goodness of fit” of the points to the curve serves as an index of the
spatial dependency—a good fit indicates strong spatial autocorrelation. The curve itself provides relative weights
for the samples surrounding a location as it is interpolated—the weights are
calculated from the equation of the curve.
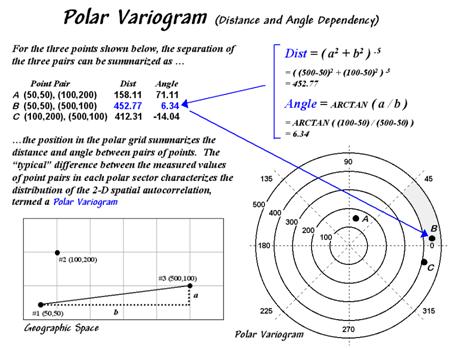
A polar variogram takes the concept a step further by considering
directional bias as well as distance. In
addition to calculating distance, the direction between point-pairs is
determined using the “opposite-over-adjacent (tangent)” geometry rule. A polar plot of the results is constructed
with rings of increasing distance divided into sectors of different angular relationships
(figure 2).
Figure
2. A polar variogram
relates the difference between sample values to both distance and direction.
Each point-pair plots within one of the sectors (shaded
portion in figure 2). The difference
between the sample values within each sector forms a third axis analogous to
the “data variation” (Y-axis) in a simple variogram.
The relative differences for the sectors serve as the weights for
interpolation. During interpolation, the
distance and angle for a location to its surrounding sample points are computed
and the weights for the corresponding sectors are used. If there is a directional bias in the data,
the weights along that axis will be larger and the matching sample points in
that direction will receive more importance.
The shape and pattern of the polar variogram surface characterizes the distance and directional dependencies in a set of data—the X and Y axes depict distance and direction between points while the Z-axis depicts the differences between sample values.
An idealized surface is lowest at the center and
progressively increases. If the shape is
a perfect bowl, there is no directional bias.
However, as ridges and valleys are formed directional dependencies are
indicated. Like a simple variogram, a
polar variogram provides a graphical representation of spatial dependency in a
data set—it just adds direction to the mix.
_____________________________
(Back to the Table of Contents)