Beyond Mapping III
|
Map
Analysis book with companion CD-ROM for hands-on exercises and further reading |
Building
Accumulation Surfaces — reviews
how proximity analysis and effective distance is used to construct accumulation
surfaces
Analyzing
Accumulation Surfaces — describes
how two surfaces can be analyzed to determine the relative travel-time
advantages
Determining
Optimal Path Corridors — describes
a technique for determining the set of the set of best paths between two points
Analyzing Stepped Accumulation Surfaces — describes
a technique for forcing an optimal path through a series of points
Note: The processing and figures discussed in this topic were derived using MapCalcTM
software. See www.innovativegis.com to download a
free MapCalc Learner version with tutorial materials for classroom and
self-learning map analysis concepts and procedures.
<Click here> for a printer-friendly version of this topic (.pdf).
(Back to the Table of Contents)
(GeoWorld, October 1997, pg. 26)
“You can’t get there from here,” is often the flippant
response when you ask directions. In many
cases it is a perfectly valid answer, as movement in geographic space is rarely
as straight forward as a straightedge.
Often there are several possible contorted paths that twist and turn in
route to a destination. However, from
the perspective of a ruler there is only one—the “shortest, straight line
connecting two points.” Several Beyond
Mapping columns1 have addressed the concepts and procedures behind
Before we get too far, a quick review might be prudent. Recall that there are primarily two ways to
represent distance in a
The splash technique tracking simple
proximity is a bit less familiar, but conceptually easy. Imagine what happens to a still pond when you
toss in a rock—splash, then one ripple away, then another, and another, until
there’s a whole set of concentric rings about the starting point. If the conditions are the same throughout the
pond, the effect is similar to nailing a ruler at the starting point and
spinning it, while scribing the set of circles formed by dragging the ruler’s
tic marks. In a raster
Now imagine tossing a handful of rocks—splash, one ripple, two ripple, three
ripple, and more radiate out from each of the starting points. When two wave-fronts meet, they stop, with
the point of interference identifying the halfway location between starting
points. The same holds true if you toss
in a set of sticks or pieces of plywood, with the ripple patterns conforming to
the irregular shapes of the objects. The
end result of all the simulated splashing and crashing in a
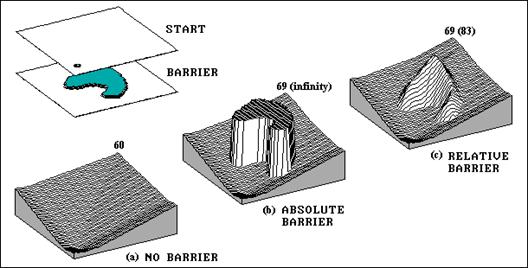
Figure 1. Accumulation surfaces showing the effects of relative and absolute barriers in mapping proximity.
Inset (a) in figure 1 is a 3-D plot of a simple proximity surface radiating from a single
point. The lowest point on the surface
contains the value 0 denoting it is “0 grid spaces away” from the start. Note that the surface is shaped like a bowl
with increasing values (1 away, 2 away, etc.).
The farthest location is in the upper right corner at a distance of 60
grid spaces * 100 meters/grid space = 6000 meters. The slight depressions along the orthogonal
and diagonal are a result of the slight directional variations in distances
computed by the “splash” algorithm.
But continuous, straight line movement forming a perfect proximity bowl is
rarely the case in the real world.
Effective proximity respects movement around and through barriers—not
“as the crow flies,” but as the crow might walk. Suppose there’s a lake in the way. Inset (b) identifies the absolute barrier
itself as being infinitely far away (fear/reality of drowning). It assigns a value of 69 grid spaces to the
farthest accessible location, indicating that the distance is a 900 meters
farther as a result of going around the lake.
The set of all map values indicate the “shortest, but not necessarily
straight” distances between the starting point and all of the other locations.
However, in winter the lake freezes and can be crossed, though at a much slower
pace on the slippery ice. It represents
a relative barrier that impedes movement, but doesn’t totally restrict
movement. Inset (c) shows the
accumulation surface assuming you walk 5 times slower on the ice. The results show that it’s still 6900 meters
to the opposite corner by going around the lake. However, if you gingerly trek to the center
of the lake, it’s equivalent to traveling 8300 meters
on open land.
Previous Beyond Mapping columns described how the
computer finds the “steepest, downhill path” along an accumulation surface to
locate the “not necessarily straight” optimal path. It’s analogous to a rain drop’s route along
the surface, which effectively retraces the wave front that got there
first. In fact, the rain drop paths from
all locations identify the “shortest, but not necessarily straight set of lines
connecting the origin to everywhere.”
Information you with a ruler, or Pythagorus
with a calculator, could never derive.
But it’s chicken-feed compared to what insights you get by analyzing the
surfaces themselves—see you next time.
_____________________
1 See
Analyzing Accumulation
Surfaces
(GeoWorld, November 1997, pg. 30-32)
The previous article
in this series described the nature of accumulation surfaces and how they are
built. Recall that the “splash”
algorithm measures distance from a starting location like waves that spread out
when a rock is tossed into a pond. The
result is a 3-dimensional surface with increasing distance reflected by the
increasing Z values stored in a matrix of grid cells. If absolute and relative barriers to movement
are introduced, these surfaces form unique shapes with ridges and peaks similar
to terrain surfaces.
However, unlike terrain surfaces, accumulation surfaces are always increasing
(no “false-bottoms”) from point, line and areal features designated as starting
locations. Areas with absolute barriers
are identified as infinitely far away and form sheer walls on an accumulation
surface. Relative barriers form hills
and ridges as they identify areas that are passable, but at an increased “cost”
(e.g., more time) per grid space. The
valleys emanating from the starting locations locate corridors of minimal
resistance to movement along the accumulation surface.
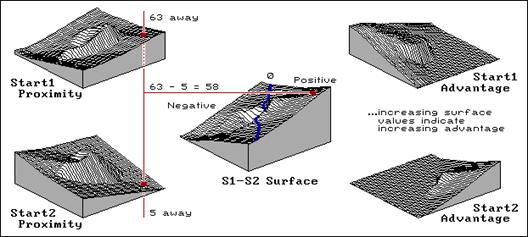
Figure 1. The difference between two
proximity surfaces identifies the relative geographic advantage between two
locations.
For example, the two
surfaces on the extreme left of figure 1 characterize movement from opposing
corners through the horseshoe-shaped relative barrier described in the previous
article. The proximity from Start1
generally increases from left to right, while the increase from Start2 is in
the opposite direction. Both surfaces
show an abrupt increase when the relative barrier is encountered, however the
shape of the resulting “hill” is different due to the different directions of
the distance waves and the shape of the barrier.
Since the horseshoe ends of the barrier face Start1, the waves easily move into
the center before interacting with the increased impedance of the barrier. The formation of a ridge indicates that some
of the waves moved around the barrier, then penetrated the barrier from the
back side. Any location along the ridge
is equally distant from the start by moving to either side of hill. The locations on the back side of the ridge,
however, are optimally connected to Start1 by moving down the hill to the right
and around the barrier… a counter-intuitive move. Neither ruler nor Pythagorous’ theorem suggest that you must initially move
away from Start1 to begin the optimal route connecting the location to Start1. That’s because they simply assume that all
movement is in a straight line connecting two points—an extremely limiting
assumption in the real world of complex barriers.
The vertical line intersecting both surfaces identifies a map location that is
63 grid spaces from Start1 and only 5 from Statrt2. Since these “shortest, but not necessarily
straight” distances are stored at the same column, row position in the two
proximity matrices, they can be easily retrieved and their difference computed
(63 - 5 = 58). If this is done for all
locations, a difference surface (S1-S2 Surface inset in the middle of the
figure) is generated identifying the relative advantage between Start1 and
Start2 access for all locations throughout the project area.
The “0” line identifies locations that are equally distant between the two
starting locations. It’s similar to the
“perpendicular bisector” you might remember from high school geometry, except
it is bent and twisted reflecting the effect of the intervening barrier on
actual movement. The sign of the
difference indicates who has the advantage—negative values identify locations
where Start1 has an advantage; positive values indicate a Start2
advantage. The magnitude of the value
identifies the strength of the advantage.
The two surfaces on the right isolate the relative advantages for both
starting locations. Similar advantage
surfaces can be derived for additional starting locations, keeping in mind that
the “starters” can be any combination of point, line or areal features.
In the example, a +58 denotes a location with a strong advantage for Start2
access… it would be stupid to trek all the way to Start1. If you were a thirsty
animal (or pub patron), why would you travel the extra distance? The liquid libations would have to be a lot
better, or the ambiance and other thirsty organisms much more to your
liking. If that were the case, then the
relative attractiveness of starter locations can be incorporated into the
derivation of the accumulation surfaces (termed “gravity” modeling).
Accumulation surface analysis provides valuable information for a wide array of
applications. Natural resource managers
use the technique to identify “home ranges” and “corridors of movement” based
on the arrangement of landscape features.
Instead assuming a simple distance of “within a two mile radius” of an animal’s
burrow, an effective distance home range based on absolute (e.g., river) and
relative (e.g., cover type preferences) barriers can modeled.
Similarly, a retail market analyst can model the “home range” of a particular
breed of shopper by characterizing the road network (e.g., speed limit) and
ancillary attractions (e.g., areas of interest). Or in-store shopper habitat can be modeled
using the aisles like roads and department fixtures as attractions; even “blue-light
specials” could be modeled as dynamic features in a real time system. Traffic flows, whether in-store, across town
or in the wild are similar beasts from a
__________________________________
Author’s
Note: for
“hands-on” experience in deriving and analyzing accumulation surfaces, see
exercises TMAP2, TUTOR5, TUTOR6 and TU-
Determining Optimal Path
Corridors
(GeoWorld, December 1997, pg. 28)
The first section in
this series described the construction and fundamental nature of accumulation
surfaces. The second section discussed an analysis procedure for mapping
relative geographic advantage that involved subtracting two surfaces. This time
we will investigate the interpretation of slope and aspect of an accumulation
surface and what information is derived if we add the surfaces.
Recall that as
distance increases from a location(s) the values can be plotted as a
3-dimensional surface, like those shown in the left portion of figure 1. The lowest point on the surface identifies
the starting location(s) as zero units away from itself. All other locations contain increasing
distance values forming the characteristic “bowl-shape” of an accumulation
surface.
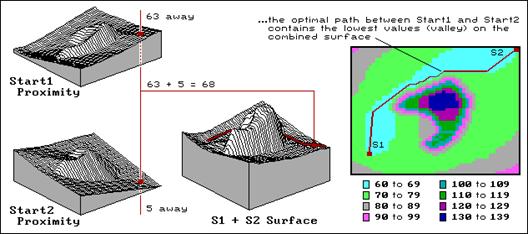
Figure 1. The sum of two proximity surfaces identifies the optimal path between two locations as the lowest values, while increasing values identify the “opportunity cost” of forcing a path through any location.
Effective distance (as
opposed to “simple,” straight-line distance) can be derived by introducing
absolute and relative barriers to movement.
The “hill” in the Starter1 and Starter2 proximity surfaces reflect the increased impedance of a horseshoe-shaped
barrier in the center of the map area.
Each grid space on a friction map is coded with the “relative cost” of
traversing that location. Note that the
increased impedance is translated into the steeper slopes for the barrier
area. Therefore a slope map of an
accumulation surface unmasks the relative ease of optimal travel through each
grid space.
The notion of “optimal movement” embedded in an accumulation surface is
important. The “splash” algorithm used to build the surface considers movement
from the eight surrounding cells to each location. The accumulated distance and the relative
impedance for each of the eight potential “steps” is
evaluated. The least costly step, in
terms of total movement, is assigned. Therefore an aspect map of an
accumulation surface unmasks the direction of optimal movement through each
grid space.
That’s a lot of spatially-specific information—the rate and direction of
optimal movement throughout a map area.
It allows us to relax the assumption that “everything moves in a
straight line and with equal impedance.”
In fact, things rarely move as simply as they respond to the complex
patterns of absolute and relative barriers existing in the real world. Slope and aspect maps of an accumulation
surface allow us to track the conditions of that complex movement at each map
location.
As described in the first article, the optimal path from any location to the
origin is identified as the steepest downhill route over the surface. In the second article, we found that
subtracting two accumulation surfaces located the bisecting line between the
origins as 0 (equidistant). The sign of
the distance value on the difference map indicated which origin was closer, and
its magnitude indicated how much closer.
For example, a
wildfire response model might generate a proximity map for two fire stations
considering both on and off-road movement.
Subtracting the maps locates the effective dividing line between the two
stations. In retail marketing, the
halfway line is extended into a broad band indicating a “combat zone” for
customers. Areas outside the band have
distinct proximity advantages, while the real battles are waged in the combat
zone where there the differences are marginal.
If subtracting accumulation surfaces creates useful information, what do you
think happens when you add them? The
surface in the center of the figure is a summation surface for the example
data. The highlighted location is 63
from Start1 and 5 from Start2, therefore it is a total
of 68 units away from both. In other
words, the best path connecting the two origins which passes through that
location has a total length of 68. In
fact, the values on the summation surface identify the length of the “best”
path forced through any given map location.
The optimal path between the two locations (identified by the line in both the
2-D and 3-D views) contains the set of locations having the lowest values (a
valley connecting the origins). The saw-toothed appearance of the optimal path
is an artifact of arithmetic rounding, the nature of the splash algorithm and
minimal friction outside the barrier in the center. Values above the valley
floor indicate the length of the best, but sub-optimal paths forced through any
location.
The difference between the lowest value on the summation surface and the value
at any other location identifies the “opportunity cost” of forcing a route
through that location. The 2-D display
shows fixed intervals of increasing opportunity cost—you would be crazy to
force a route through the darker tones (a mountain of opportunity cost). Next time we will look at constructing a
“stepped accumulation surface” which enables you to determine the optimal path
connecting a series of predetermined stops along the way. As a sneak preview, it involves minimizing
successive accumulation surfaces… whew!
Analyzing Stepped
Accumulation Surfaces
(GeoWorld, January 1998, pg. 30)
Hopefully you have
survived the last three columns on accumulation surfaces. The discussion has covered the fundamental
nature of accumulation surfaces (increasing distance waves), procedures for
determining relative geographic advantage (subtract), ways to uncover direction
and speed of optimal movement (slope and aspect), and a technique for
determining the corridor of optimal movement (add). If that wasn’t enough, now we get to extend
the discussion to a “stepped accumulation surface” and “optimal path zones.”
Suppose you know several places you would like to visit, but don’t have a
particular route in mind. If you know
the order you would like to visit them, then a directed stepped accumulation
surface is for you. Simply generate an
effective proximity surface from the first location like those discussed in the
previous articles—splash, one ripple, two ripple, three ripple and more radiate
out from your starting point. The
familiar bowl of proximity identifies the effective distance to all other
locations. All you have to do is
“stream” down the bowl from your second point of interest to identify the
optimal path.
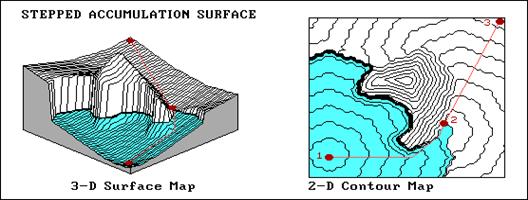
Figure 25.4. Stepped Accumulation Surface. Proximity from the first point is calculated (shaded) until the second point is reached, then proximity from that point is calculated (non-shaded) forming the next tier; the individual optimal paths along each of the stepped proximity surfaces forms the overall optimal route.
Now, construct a
proximity surface from the second point to everywhere, and stream your third
stop down it for the second leg of your journey. The left side of Figure 1 shows a stepped
accumulation surface for the first two segments of a “directed hike” through
the demonstration area. The shaded area
shows the portion of the proximity surface from the start until the concentric
ripples encountered the second point.
The non-shaded area picks up the count by adding the proximity from
there to all other locations. The result
is a two-tiered surface similar to a spiral staircase. If you stream down the stepped accumulation
surface from the third stop, it first flows down the top tier to the second
stop, then continues down to the first point (right side of Figure 1).
Additional stops are
considered by repeating the successive construction of “proximity bowls” and
streaming down them for sequential optimal path segments. An undirected procedure allows the computer
to determine a spatially efficient ordering of the points. You simply identify a starting location, the
points you need to visit and the computer calculates the optimal route
connecting them. The solution spreads
out from the first point until it encounters the closest visitation point, then
streams down the truncated proximity surface for the first leg. The next tier spreads out until it encounters
its closest point and streams down for the next leg. The process continues until all of the
visitation points have been evaluated.
If you intend to return to the starting point, the home leg considers
the starting point and is evaluated last.
The undirected, stepped accumulation surface technique (whew …quite a mouthful)
is similar to the classic “traveling salesman” problem in network
analysis. However, it provides a
solution in continuous space, respecting the complex reality of absolute and
relative barriers. This is important if
the traveling salesman doesn’t have a car, or if the mover isn’t constrained to
a bunch of lines, like a herd of elk, or shoppers in a store.
In a recent project (see Author’s Note), we encoded the floor plan for a retail
superstore (98,000 1-foot grids), translating the fixtures into absolute
barriers and congested areas into relative barriers. Shelving locations were identified on each
fixture and linked to product codes. The
checkout records for each market basket were used to “place” each item
purchased on the appropriate shelf.
These visitation points were evaluated for the “plausible” path used to
collect the items between the door to the cash
register.
Granted, a shopper
could do “a random walk” to collect the items, but a shopper with a mission who
knows the store, would be foolish to veer off the calculated route. Also, the consideration of several thousands
of paths over a period of time converges on a map of relative in-store shopper
activity. The analysis was summarized in
hourly time-steps, displayed as normalized thematic maps, and animated to show
the ebb and flow of shopper activity throughout the day.
The right side of Figure 2 shows the zones of influence for each leg of the
optimal route. The locations within each
zone are optimally connected to a particular segment. So, how might one use such information? In the shopper example, the distance from a
shopper’s path can be interpreted as geographic impedance that must be overcome
to veer off stride. Influence zones
locate areas along a common portion of a shopper’s route. Overlaying these data with in-store
departments, sales density surfaces and item categories produces a lot of
information about shelving for retail marketing types. How might you use accumulation surfaces?
…it’s up to your innovative mind.
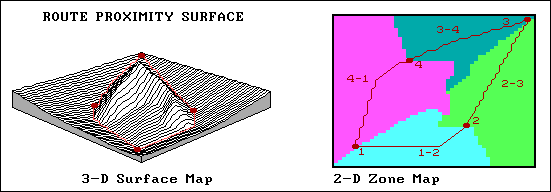
Figure 2. Route Proximity Surface. Proximity from the optimal route identifies the distance to the closest segment of the route for every location in a project area; the influence zone of each segment along the route identifies which segment is the closest.
_________________________
Author’s Note: see www.innovativegis.com/basis/mapanalysis
/, Topic 6, “Analyzing In-Store Shopping Patterns.”
(Back to the Table of Contents)