|
Topic 7 – Overlaying Maps and
Summarizing the Results |
Beyond Mapping book |
Characterizing Spatial Coincidence the Computer’s
Way — describes point-by-point overlay techniques
Map Overlay Techniques— there’s more than one
— discusses region-wide summary
and map coincidence techniques
If I Hadn’t of Believed It, I Wouldn’t Have Seen It — discusses
map-wide overlay techniques and the spatial evaluation of algebraic equations,
such as regression
Note: The processing
and figures discussed in this topic were derived using MapCalcTM software. See www.innovativegis.com to
download a free MapCalc Learner version with tutorial materials for classroom
and self-learning map analysis concepts and procedures.
<Click here>
right-click to download a printer-friendly version of this topic (.pdf).
(Back to the Table of Contents)
______________________________
Characterizing Spatial Coincidence
the Computer’s Way
(GIS World,
Jan/Feb 1992)
...that’s the Beauty of the Pseudo-Sciences, since
they don't depend on empirical verification, anything can be explained
(Doonesbury).
As
noted in many previous sections, GIS maps are numbers and a rigorous,
quantitative approach to map analysis should be maintained. However, most of our prior experience with
maps is non-quantitative, using map sheets composed of inked lines, shadings,
symbols and zip-a-tone. We rarely think
of map uncertainty and error propagation.
And we certainly wouldn't think of demanding such capabilities in our
GIS software. That is, not as of yet.
Everybody knows the 'bread and butter' of a GIS is its ability to overlay maps. Why it's one of the first things we think of asking a vendor (right after viewing the 3-D plot that knocks your socks off). Most often the question and the answer are framed in our common understanding of "light-table gymnastics." We conceptualize peering through a stack of acetate sheets and interpreting the subtle hues of resulting colors. To a GIS you're asking the computer to identify the condition from each map layer for every location in a project area. From the computer's perspective, however, this is simply one of a host of ways to characterize the spatial coincidence.
Let's
compare how you and your computer approach the task of identifying
coincidence. Your eye moves randomly
about the stack, pausing for a nanosecond at each location and mentally
establishing the conditions by interpreting the color. Your summary might conclude that the
northeastern portion of the area is unfavorable as it has "kind of a
magenta tone." This is the result
of visually combining steep slopes portrayed as bright red with unstable soils
portrayed as bright blue with minimal vegetation portrayed as dark green. If you want to express the result in map
form, you would tape a clear acetate sheet on top and delineate globs of color
differences and label each parcel with your interpretation. Whew!
No wonder you want a GIS.
The
GIS goes about the task in a very similar manner. In a vector system, line segments defining
polygon boundaries are tested to determine if they cross. When a line on one map crosses a line on
another map, a new combinatorial polygonal is indicated. Trigonometry is employed, and the X,Y coordinate of the intersection of the lines is
computed. The two line segments are
split into four and values identifying the combined map conditions are
assigned. The result of all this
crossing and splitting is the set of polygonal prodigy you so laboriously
delineated by hand.
A
raster system has things a bit easier.
As all locations are predefined as a consistent set of cells within a
matrix, the computer merely 'goes' to a location, retrieves the information
stored for each map layer and assigns a value indicating the combined map
conditions. The result is a new set of
values for the matrix identifying the coincidence of the maps.
The
big difference between ocular and computer approaches to map overlay isn't so
much in technique, as it is in the treatment of the data. If you have several maps to overlay you
quickly run out of distinct colors and the whole stack of maps goes to an indistinguishable
dark, purplish hue. One remedy is to
classify each map layer into just two categories, such as suitable and
unsuitable. Keep one as clear acetate
(good) and shade the other as light grey (bad).
The resulting stack avoids the ambiguities of color combinations, and
depicts the best areas as lighter tones.
However, in making the technique operable you have severely limited the
content of the data-- just good and bad.
The
computer can mimic this technique by using binary maps. A "0" is assigned to good
conditions and a "1" is assigned to bad conditions. The sum of the maps has the same information
as the brightness scale you observe-- the smaller the value the better. The two basic forms of logical combination
can be computed. "Find those
locations which have good slopes .AND. good soils .AND. good vegetative
cover." Your eye sees this as the
perfectly clear locations. The computer
sees this as the numeric pattern 0-0-0.
"Find those locations which have good slopes .OR. good soils .OR. good vegetative
cover." To you this is could be any
location that is not the darkest shading; to the computer it is any numeric
pattern that has at least one 0. But how
would you handle, "Find those locations which have good slopes .OR. good soils .AND. good vegetative cover"? You can't find them by simply viewing the
stack of maps. You would have to spent a lot of time flipping through the stack. To the computer, this is simply the patterns
0-1-0, 1-0-0 and 0-0-0. It's a piece of
cake from the digital perspective.
In
fact any combination is easy to identify.
Let's say we expand our informational scale and redefine each map from
just good and bad to not suitable (0), poor (1), marginal (2), good (3) and
excellent (4). We could ask the computer
to INTERSECT SLOPES WITH SOILS WITH COVER COMPLETELY FOR ALL-COMBINATIONS. The result is a map indicating all
combinations that actually occur among the three maps. Likely this map would be too complex for
human viewing enjoyment, but it contains the detailed information basic to many
application models. A more direct
approach is a geographic search for the best areas invoked by asking to
INTERSECT SLOPES WITH SOILS WITH COVER FOR EXCELLENT-AREAS ASSIGNING 1 TO 4 AND
4 AND 4. Any combination not assigned a
value drops to 0, leaving a map with 1's indicating the excellent areas.
Let's
try another way of combining these maps by asking to COMPUTE SLOPES MINIMIZE
SOILS MINIMIZE COVER FOR WEAK-LINK. The
resulting map's values indicate the minimal coincidence rating for each
location. Low values indicate areas of
concern and a 0 indicate areas to dismiss as not suitable from at least one
map's information. There is a host of other
computational operations you could invoke, such as plus, minus, times, divided,
and exponentiation. Just look at the
functional keys on your hand calculator.
But you may wonder, "why would someone
want to raise one map to the power of another"? Spatial modelers who have gone beyond
mapping, that's who.
What
would happen if, for each location (be it a polygon or a cell), we computed the
sum of the three maps, then divided by the number of
maps? That would yield the average
rating for each location. Those with the
higher averages are better. Right? You might want
to take it a few steps further. First,
in a particular application, some maps may be more important than others in
determining the best areas. Ask the
computer to AVERAGE SLOPES TIMES 5 WITH SOILS TIMES 3 WITH COVER TIMES 1 FOR
WEIGHTED-AVERAGE. The result is a map
whose average ratings are more heavily influenced by slope and soil
conditions.
Just
to get a handle on the variability of ratings at each location, you can
determine the standard deviation-- either simple or weighted. Or for even more information, determine the
coefficient of variation, which is the ratio of the standard deviation to the
average, expressed as a percent. What
will that tell you? It hints at the
degree of confidence you should put into the average rating. A high COFFVAR indicates wildly fluctuating
ratings among the maps and you might want to look at the actual combinations
before making a decision.
How
about one final consideration? Combine
the information on minimal rating (WEAKEST-LINK) with that of the average
rating (WEIGHTED-AVERAGE). A prudent
decision-maker would be interested in those areas with the highest average
rating, but score at least 2 (marginal) in any of the map layers. This level of detail should be running
through your head while viewing a stack of acetate sheets, or a simple GIS
product depicting map coincidence. Is
it? If not, you might consider stepping
beyond mapping.
_____________________
As with all Beyond Mapping articles, allow me to apologize in advance for the "poetic license" invoked in this terse treatment of a technical subject. Readers interested in more information should read a "classic" paper in map overlay by Charles J. Robinove entitled "Principles of Logic and the Use of Digital Geographic Information Systems," published by U.S. Geological Survey, 1977.
Map Overlay Techniques— there’s
more than one
(GIS
World, March 1992)
…I
have the feeling we aren’t in Kansas anymore (Dorothy to Todo).
Last
section's discussion of map overlay procedures may have felt like a scene from
the Wizard of Oz. The simple concept of
throwing a couple of maps on a light-table was blown all out of proportion into
the techy terms of combinatorial, computational and statistical summaries of
map coincidence. An
uncomfortable, unfriendly and unfathomable way of thinking. But that's the reality of GIS-- the
surrealistic world of map-ematics.
Now
that maps are digital, all GIS processing is the mathematical or statistical summary
of map values. What characterized last
issue's discussion was that the values to be summarized were obtained from a
set of spatially registered maps at a particular location, termed point-by-point
map overlay. Like the movie
TRON, imagine you shrank small enough to crawl into your computer and found
yourself standing atop a stack of maps.
You look down and see numbers aligned beneath you. You grab a spear and thrust it straight down
into the stack. As you pull it up, the
impaled values form a shish kabob of numbers.
You run with the kabob to the CPU and mathematically or statistically
summarize the numbers as they are pealed off. Then you run back to the stack, place the
summary value where you previously stood, and then move over to next cell in a
raster system. Or, if your using a vector system, you would move over to the next
'polygonal prodigy' (see last issue).
What
filled the pages last issue, were some of ways to summarize the values. Let's continue with the smorgasbord of
possibilities. Consider a 'coincidence
summary' identifying the frequency of joint occurrence. If you CROSSTAB FORESTS WITH SOILS a table
results identifying how often each forest type jointly occurs with each soil
type. In a vector system, this is the
total area of all the polygonal prodigy for each of
the forest/soil combinations. In a
raster system, this is simply a count of all the cell locations for each
forest/soil combination.
|
TABLE 1.
Coincidence Table
For Map1 = FORESTS With
Map2 = SOILS |
||||||||
|
Map1 Forests |
Number of Cells |
Map1 Soils |
Number of Cells |
|
Number of Crosses |
Percent of 625 Total |
% of Map 1 |
% of Map 2 |
|
1 Deciduous |
303 |
1 Lowland |
427 |
|
299 |
47.84 |
98.68 |
70.02 |
|
1 Deciduous |
303 |
2 Upland |
198 |
|
4 |
0.64 |
1.32 |
2.02 |
|
2 Conifer |
322 |
1 Lowland |
427 |
|
128 |
20.48 |
39.75 |
29.98 |
|
2 Conifer |
322 |
2 Upland |
198 |
|
194 |
31.04 |
60.25 |
97.98 |
For
example, reading across the first row of Table 1 notes that Forest category 1
(Deciduous) contains 303 cells distributed throughout the map. The Soils category 1
(Lowland) totals 427 cells. The
next section of the table notes that the joint condition of Deciduous/Lowland
occurs 299 times for 47.84 percent of the total map area. Contrast this result with that of
Deciduous/Upland occurrence on the row below indicating only four 'crosses' for
less than one percent of the map. The
coincidence statistics for the Conifer category is more balanced with 128 cells
(20.48%) occurring with the Lowland soil type and 194 cells (31.04%) occurring with the Upland soil type.
These
data may cause you to jump to some conclusions, but you had better consider the
right side of the table before you do.
These columns normalize the coincidence count to the total number of
cells in each category. For example, the 299 Deciduous/Lowland coincidence accounts for
98.68 percent of all occurrences of Deciduous trees ((299/303)*100). That's a very strong relationship. However, from Lowland soil occurrence the 299
Deciduous/Lowland coincidence is a bit weaker as it accounts for only 70.02
percent of all occurrences of Lowland soils ((299/427)*100). In a similar vein, the Conifer/Upland
coincidence is very strong as it accounts for 97.98 percent of the occurrence
of all Upland soil occurrences. Both
columns of coincidence percentages must be considered as a single high percent
might be merely the result of the other category occurring just about
everywhere.
Whew! What a bunch of droning gibberish. Maybe you had better read that paragraph
again (and again...). It's important, as
it is the basis of spatial statistic's concept of "correlation"-- the
direct relationship between two variables.
For the non-techy types seeking just 'the big picture,' the upshot is
that a coincidence table provides insight into the relationships among map
categories. A search of the table for
unusually high percent overlap of map categories uncovers strong positive
relationships. Relatively low percent
overlap indicates negative relationships.
The
one and two percent overlaps for Deciduous/Upland suggests the trees are
avoiding these soils. I wonder what
spatial relationship exists for Spotted Owl activity and forest type? For Owl activity and human activity? For convenience store
locations and housing density? For incidence of respiratory disease and proximity to highways?
There
are still a couple of loose ends before we can wrap-up point-by-point overlay
summaries. One is direct map comparison,
or 'change detection'. For
example, if you encode a series of land use maps for an area, then subtract
each successive pair of maps, the locations that
underwent change will appear as non-zero values for each time step. In GIS-speak, you would enter COMPUTE
LANDUSE-T2 MINUS LANDUSE-T1 FOR CHANGE-T2&1 for a map of the land use
change between Time 1 and Time 2.
If
you are real tricky and think 'digitally,' you will assign a binary progression
to the land use categories (1,2,4,8,16, etc.), as the
differences will automatically identify the nature of the change. The only way you can get a 1 is 2-1; a 2 is
4-2; a 3 is 4-1; a 6 is 8-2; etc. A
negative sign indicates the opposite change, and now all bases are
covered. Prime numbers will also work,
but they require more brain power to interpret.
Our
last point-by-point operation is a weird one-- 'covering'. This operation is truly spatial and has no
traditional math counterpart. Imagine
you prepared two acetate sheets by coloring all of the forested areas an opaque green on one sheet and all of the roads an opaque
red on the other sheet. Now overlay them
on a light-table. If you place the
forest sheet down first the red roads will 'cover' the green forests and you
will see the roads passing through the forests.
If the roads map goes down first, the red lines will stop abruptly at
the green forest globs.
In
a GIS, however, the colors become numbers and the clear acetate is assigned
zero. The command COVER FORESTS WITH
ROADS causes the computer to go to a location and assess the shish kabob of
values it finds. If the kabob value for
roads is 0 (clear), keep the forest value underneath it. If the road value is non-zero, place that
value at the location, regardless of the value underneath.
So
What? What's it good for? There is a lot of advanced modeling uses,
however covering is most frequently used for masking map information. Say you just computed a slope map for a large
area and you want to identify the slope for just your district. You would create a mask by assigning 0 to
your district and some wild number like 32,000 to the area outside your
district. Now cover the slope map with
your mask and the slopes will show through for just your district. This should be a comfortable operation. It is just like you do on the light-table.
But so much for that comfortable feeling. Let's extend our thinking to region-wide
map overlay. Imagine you're back
inside your computer, but this time you end up sandwiched between two
maps. It's a horrible place and you are
up to your ankles in numbers. You glance
up and note there is a pattern in the numbers on the map above. Why it is the exact shape of your
district! This time you take the spear
and attach a rope, like an oversized needle and thread. You wander around threading the numbers at
your feet until you have impaled all of them within the boundary of your
district. Now run to the CPU, calculate
their average and assign the average value to your district. Voila, you now know the average slope for
your district provided you were sloshing around in slope values.
Since
you're computerized and moving a megahertz speed, you decide to repeat the
process for all of the other districts denoted on the template map above
you. You are sort of a digital
cookie-cutter summarizing the numbers you find on one map within the boundaries
identified on another map. That's the
weird world of region-wide map overlay.
In GIS-speak, you would enter COMPOSITE DISTRICTS WITH SLOPE AVERAGE.
However,
average isn't the only summary you can perform with your lace of numbers. Some other summary statistics you might use
include total, maximum, minimum, median, mode or minority value; the standard
deviation, variance or diversity of values; and the correlation, deviation or
uniqueness of a particular combination of values. See, math and stat are the cornerstones of
GIS.
For
example, a map indicating the proportion of undeveloped land within each of
several counties could be generated by superimposing a map of county boundaries
on a map of land use and computing the ratio of undeveloped land to the total
land area for each county. Or a map of
postal codes could be superimposed over maps of demographic data to determine
the average income, average age and dominant ethnic group within each zip
code. Or a map of dead timber stands
could be used as a template to determine average slope, dominant aspect,
average elevation and dominant soil for each stand. If they tend to be dying at steep, northerly,
high elevations on acidic soils this information might help you locate areas of
threatened living trees that would benefit from management action. Sort of a preventative
health plan for the woods.
In
the next section, point-by-point and region-wide overlaying will be extended to
concepts of map-wide overlay. If all
goes well, this will complete our overview of map overlay and we can forge
ahead to other interesting (?) topics.
_____________________
As
with all Beyond Mapping articles, allow me to
apologize in advance for the "poetic license" invoked in this terse
treatment of a technical subject.
Readers interested in an in-depth presentation of this material should
consult a recent text entitled "Statistics for Spatial Data," by Noel
Cressie, Wiley Series in Probability and Mathematical
Statistics, 1991.
If I Hadn’t Believed It, I
wouldn’t have Seen It
(GIS
World, April 1992)
…isn’t
that the truth, as prejudgment often determines what we see in a map (as well
as a ppsychologist’s Rorschach
inkblot test).
For better or worse, much of map analysis is left to
human viewing.
In many ways the analytical power of the human mind far exceeds the
methodical algorithms of a GIS. As your
eye roams across a map, you immediately assess the relationships among spatial
features, and your judgment translates these data into meaningful
information. No bits, bytes or buts, that's the way it is. Just as you see it.
Recently,
I had an opportunity to work with an organization that had acquired a major GIS
software package, developed an extensive database over a period of several
months and had just begun using the system in decision-making. From the more than one hundred map layers in
the database, three composite maps were generated for each of the eighteen topo sheets covering the project area. The three maps were aligned on top of each
other and a fourth clear acetate sheet was attached to complete the
bundle.
The
eighteen map bundles, in turn, were edge-matched and taped along the wall of a
local gymnasium. A group of
decision-makers strolled down the gallery of maps, stopping and flipping
through each bundle as they went. A
profusion of discussion ensued. Finally,
with knitted brows and nodding heads, annotations were sketched onto the clear
top sheet designating areas available for logging, for development, for
wildlife habitat, for recreation, and a myriad of other land uses. The set of 'solution' sheets were peeled off
the top and given to the stunned GIS specialists to be traced into the GIS for
final plotting.
Obviously,
map overlay means different things to different people. To the decision-makers it provided a 'data
sandwich' for their visual analysis. To
the GIS specialists it not only organizes and displays map composites, but it
provides new analytic tools. To readers
of the last couple of issues it means combinatorial, computational and
statistical summaries of map coincidence.
As noted, the coincidence data to be summarized can be obtained by point-by-point
or region-wide map overlay techniques.
With
those discussions behind us, we move on to a third way of combining maps-- map-wide
overlay. Recall that point-by-point
overlay can be conceptualized as vertically "spearing" a shish kabob
of numbers for each location on a set of registered maps. By contrast, region-wide overlay horizontally
"laces" a string of numbers within an area identified on another
map. Now are you ready for this,
map-wide overlay can be thought of as "plunging" an equation through
a set of registered maps. In this instance
each map is considered a variable, each location is considered a case and each
value is considered a measurement. These
terms (variable, case and measurement) hold special significance for techy
types, and have certain rights, privileges and responsibilities when evaluating
equations. For the rest of us, it means
that the entire map area is summarized in accordance of an equation.
For
example, map-wide overlay can be used for comparing two maps. Traditional statistics provides several
techniques for assessing the similarity among sets of numbers. The GIS provides the organization of the
number sets-- cells in a raster system and polygonal prodigy in a vector
system. A simple "t" or
"F" Test uses the means and variances of two sample populations to
determine if you can statistically say "they came from the same
mold." Suppose two sample
populations of soil lead concentration cover the same map area for two
different time periods. Did lead
concentration "significantly" change?
Map-wide comparison statistics provides considerable insight.
Another
comparison technique is similarity.
Suppose you have a stack of maps for the world depicting the Gross
National Product, Population Density, Animal Protein Consumption and other
variables describing human living conditions.
Which areas are similar and which areas are dissimilar? In the early 1980's I had a chance to put
this approach into action. The concept
of "regionalism" had reached its peak and the World Bank was
interested in ways it could partition the world into similar groupings. A program was developed allowing the user to
identify a location (say Northeastern Nigeria) and generate a map of similarity
for all other locations of the world.
The similarity map contained values from 0 (totally dissimilar) to 100
(identical).
A
remote sensing specialist would say "so what, no big deal." It is a standard multivariate classification
procedure. Spear the characteristics of
the area of interest (referred to as a feature vector) and compare this response
pattern to those of every other location in the map area. They're right, it is no big deal. All that is needed is scale adjustments to
normalize map response ranges. The rest
is standard multivariate analysis.
However, to some it is mind wrenching because we normally do not mix map
analysis and multivariate classification in the same breadth. But that's before the digital map took us
beyond mapping.
Let's
try another application perspective. A
natural resource manager might have a set of maps depicting slope, aspect, soil
type, depth to bedrock, etc. Which areas
are similar and which areas are dissimilar?
The procedure is like that described above. In this instance, however, clustering
techniques are used to group locations of similar characteristics. Techy terms of "intra- and inter-cluster
distances in multivariate space" report the similarities. To the manager, the map shows ecological
potential-- a radically different way to carve-up the landscape.
Chances
are the current carving into timber management units was derived by aerial
photo interpretation. Some of the
parcels are the visible result of cut-out/get-out logging and forest fires
which failed to respect ecological partitions.
Comparison of the current management parcels to the ecological groupings
might bring management actions more into line with Mother Nature. The alternative is to manage the woods into
perpetuity based on how the landscape exposed itself to aerial film several
years back.
In
addition to comparison and similarity indices, predictive equations can be
evaluated. For example, consider an old
application done in the late 1970's. A
timber company in the Pacific Northwest was concerned in predicting
"timber felling breakage." You
see, when you cut a tree there is a chance it will crack when it hits the
ground. If it cracks, the
sawmill will produce little chunks of wood instead large, valuable
boards. This could cost you
millions. Where should you send your
best teams with specialized equipment to minimize breakage?
Common
sense tells you if there are big old rotten trees on steep slopes expect
kindling at the mill. A regression
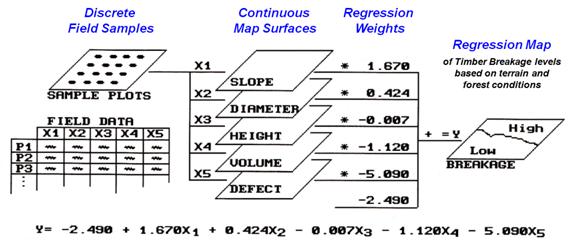
equation specifies this bit more rigorously as
Y= -2.490 + 1.670X1 + 0.424X2 - 0.007X3 -
1.120X4 - 5.090X5
where Y= predicted
timber felling breakage and X1= percent slope, X2= tree diameter,
X3= tree height, X4= tree volume and
X5= percent defect
Now
you go to the woods and collect data at several sample plots, and then
calculate the average for each variable.
You substitute the averages into the equation and solve. There that's it, predicted timber felling
breakage for the proposed harvest unit.
If it is high, send in the special timber beasts. If it is low, send them elsewhere.
But
is it really that simple? What if there
are big trees to the north and little trees to the south? There must be medium-sized trees (average)
everywhere is the assumption of your analytic procedure. And what if it is steep to the north and
fairly flat to the south? Why it must be
moderately sloped (average) everywhere is the assumption. This reasoning leads to medium-sized trees on
moderate slopes everywhere. Right? But hold it,
let's be spatially specific-- there are big trees on steep slopes to the
north. This is a real board and profit
busting condition. Your field data is
trying to tell you this, yet your non-spatial analysis blurs the information
into typical responses assumed everywhere the same.
Figure
1.Schematic of spatially evaluating prediction equations.
As
depicted in figure 1, a spatial analysis first creates continuous surface maps
from the field data (see Beyond Mapping column, October, 1990). These mapped variables, in turn, are
multiplied by their respective regression coefficients and then summed. The result is the spatial evaluation of the
regression equation in the form of a map of timber felling breakage. Not a single value assumed everywhere, but a
map showing areas of higher and lower breakage.
That's a lot more guidance from the same set of field data.
In
fact further investigation showed the overall average of the map predictions
was very different from the non-spatial prediction. Why?
It was due to our last concept-- spatial autocorrelation. The underlying assumption of the non-spatial
analysis is that all of the variables of an equation are independent. Particularly in natural resource applications
this is a poor assumption. People,
birds, bears and even trees tend to spatially select their surroundings. It is rare that you find any resource
randomly distributed in space. In this
example, there is a compelling and easily explainable reason for big trees on
steep slopes. During the 1930's the area
was logged and who in their right mind would hassle with the trees on the steep
slopes. The loggers just moved on to the
next valley, leaving the big trees on the steeper slopes-- an obvious
relationship, or more precisely termed, spatial autocorrelation. This condition affects many of our
quantitative models based on geographic data.
So
where does all this lead? To at least an
appreciation that map overlay is more than just a data sandwich. The ability to render graphic output from a
geographic search is just the beginning of what you can do with the map overlay
procedures embedded in your GIS.
_______________________________________

(Back to the Table of Contents)